技术摘要：
本发明公开了一种牛顿‑拉弗森算法的子通道求解方法，包括：进入第一个轴向层；通过对轴向动量方程、横向动量方程得到轴向压降与流量的关系式以及横向压差与流量的关系式；将关系式代入给定的质量守恒方程得到关于当前轴向层压降的方程组；根据方程组得到当前轴向层各  全部
背景技术：
COBRA最初由Pacific  Northwest实验室于1980年开发。自此以后，各类学术和工 业组织进一步发展代码，产生许多变体，如COBRA-TF。COBRA-TF用于CASL开发的反应堆应用 堆芯模拟器(VERA-CS)虚拟环境中的子通道热工水力求解。COBRA-TF是基于两流体模型的 瞬态程序。包含蒸汽，连续液体和夹带液滴的质量、能量和动量守恒方程，共9个方程。能对 堆芯中的固体结构(如未加热的热构件和燃料棒)以及流体进行建模。由于包含正常(单相、 小气泡和大气泡)和热壁(反环状流、弥散液滴和降液膜)的本构关系，既可以计算正常运行 工况，也可以计算事故工况(失水事故)，还包括空泡漂移、湍流交混和格架换热增强等模 型。但COBRA-TF的求解效率较低且稳定性较差。
技术实现要素：
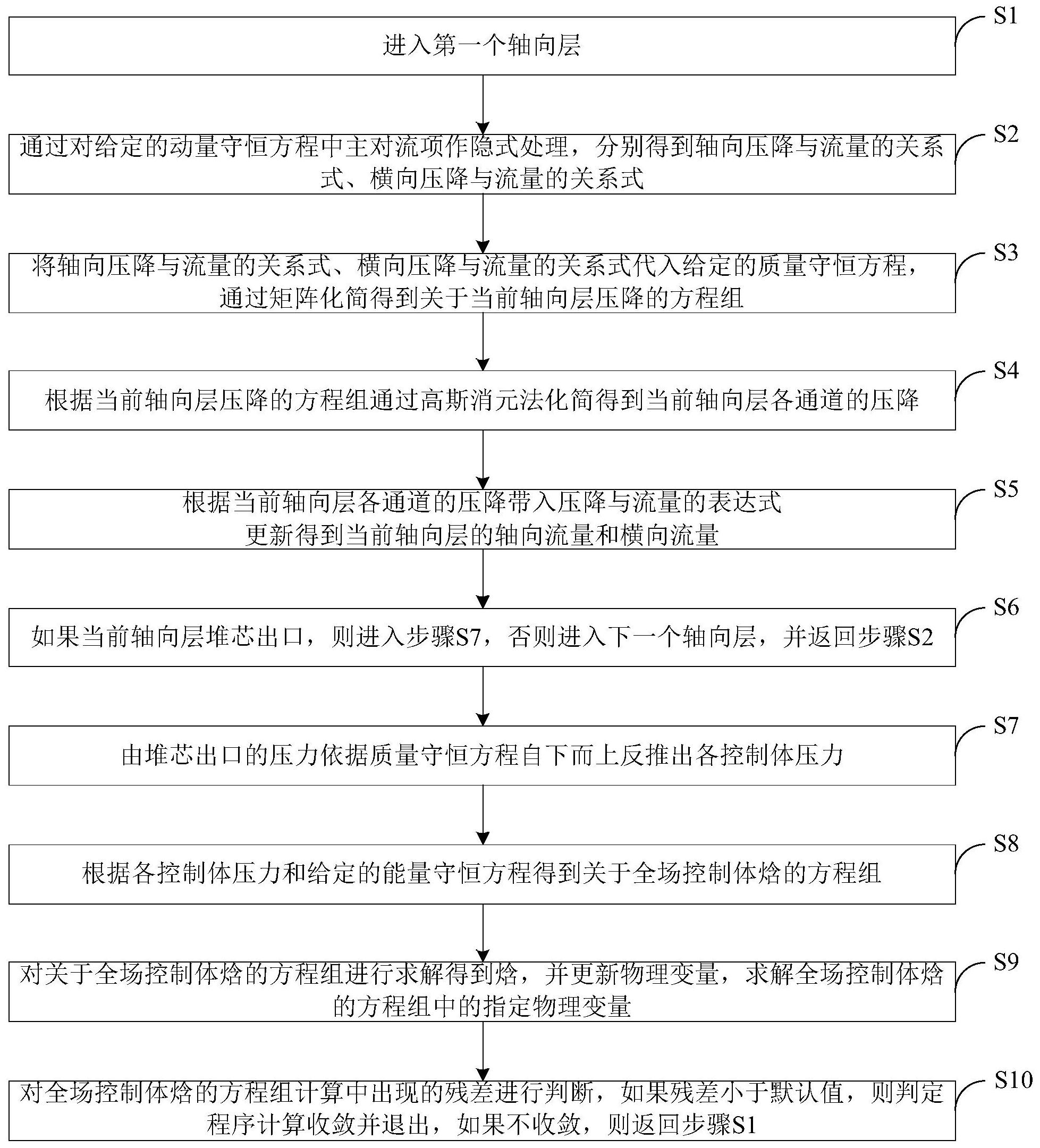
本发明旨在至少解决上述技术问题之一。 为此，本发明的目的在于提出一种牛顿-拉弗森算法的子通道求解方法，可以增加 的求解效率以及稳定性。 为了实现上述目的，本发明的实施例公开了一种牛顿-拉弗森算法的子通道求解 方法，包括以下步骤：S1：进入第一个轴向层；S2：通过对轴向动量方程、横向动量方程中主 对流项作隐式处理，分别得到轴向压降与流量的关系式以及横向压差与流量的关系式；S3： 将轴向压降与流量的关系式、横向压差与流量的关系式代入给定的质量守恒方程，通过矩 阵化简得到关于当前轴向层压降的方程组；S4：根据所述当前轴向层压降的方程组通过高 斯消元法化简得到所述当前轴向层各通道的压降；S5：根据所述当前轴向层各通道的压降 带入压降与流量的表达式更新得到所述当前轴向层的轴向流量和横向流量；S6：如果当前 轴向层堆芯出口，则进入步骤S7，否则进入下一个轴向层，并返回步骤S2；S7：由所述堆芯出 口的压力依据所述质量守恒方程自下而上反推出各控制体压力；S8：根据所述各控制体压 力和给定的能量守恒方程得到关于全场控制体焓的方程组；S9：对所述关于全场控制体焓 的方程组进行求解得到焓，并更新物理变量，求解所述全场控制体焓的方程组中的指定物 理变量；S10；对所述全场控制体焓的方程组计算中出现的残差进行判断，如果所述残差小 于默认值，则判定程序计算收敛并退出，如果不收敛，则返回步骤S1。 根据本发明实施例的牛顿-拉弗森算法的子通道求解方法，通过稳态算法和瞬态 算法并行的形式，增加的求解效率以及稳定性。 另外，根据本发明上述实施例的牛顿-拉弗森算法的子通道求解方法还可以具有 如下附加的技术特征： 可选地，所述给定的质量守恒方程为： 4 CN 111723451 A 说　明　书 2/6 页 其中，ρm为混合密度， 为混合速度。 可选地，所述给定的能量守恒方程为： 其中，hm为混合相的焓，p为总压， 为壁面传热及湍流换热项，Φ为热源项。 本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变 得明显，或通过本发明的实践了解到。 附图说明 本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得 明显和容易理解，其中： 图1是本发明一个实施例的牛顿-拉弗森算法的子通道求解方法的流程图； 图2(a)-2(d)是本发明一个实施例中给定边界条件时生成功率变化曲线的示意 图； 图3(a)-3(c)是本发明一个实施例中子通道t＝1.0s时压降、温度、流量沿程分布 的对比结果图； 图4(a)-4(c)是本发明一个实施例中子通道t＝2.0s时压降、温度、流量沿程分布 的对比结果图； 图5(a)-5(c)是本发明一个实施例中子通道t＝2.0s时压降、温度、流量沿程分布 的对比结果图； 图6(a)-6(c)是本发明一个实施例中子通道t＝2.0s时压降、温度、流量沿程分布 的对比结果图。