技术摘要：
本申请公开了一种覆盖底泥的铺盖临界失稳厚度的计算方法及系统，其中，计算方法包括如下步骤：建立铺盖临界失稳厚度计算模型；利用气体溶解度算法求解所述铺盖临界失稳厚度计算模型，得到铺盖临界失稳厚度。本申请提供的铺盖临界失稳厚度计算方法，可以快速求解得到铺  全部
背景技术：
铺盖技术是一种底泥的原位物理修复方法，通过在底泥上放置覆盖物，使底泥与 水体隔离，防止底泥污染物向水体迁移。现有底泥原位铺盖技术普遍关心铺盖材料的性能， 对于底泥铺盖的稳定分析方法未有涉及，然而底泥铺盖的稳定分析也是一个在设计中不可 忽视的问题。若为达到底泥修复目的，盲目的采用过厚的铺盖层，造成底泥铺盖系统失稳， 将产生较大安全隐患。 因此，本发明提出了一种底泥铺盖临界失稳厚度的快速计算方法，通过编程计算， 输入底泥参数与底泥铺盖材料相关参数，可在几秒之内快速计算出底泥铺盖临界失稳厚 度，为底泥铺盖的设计提供依据。
技术实现要素：
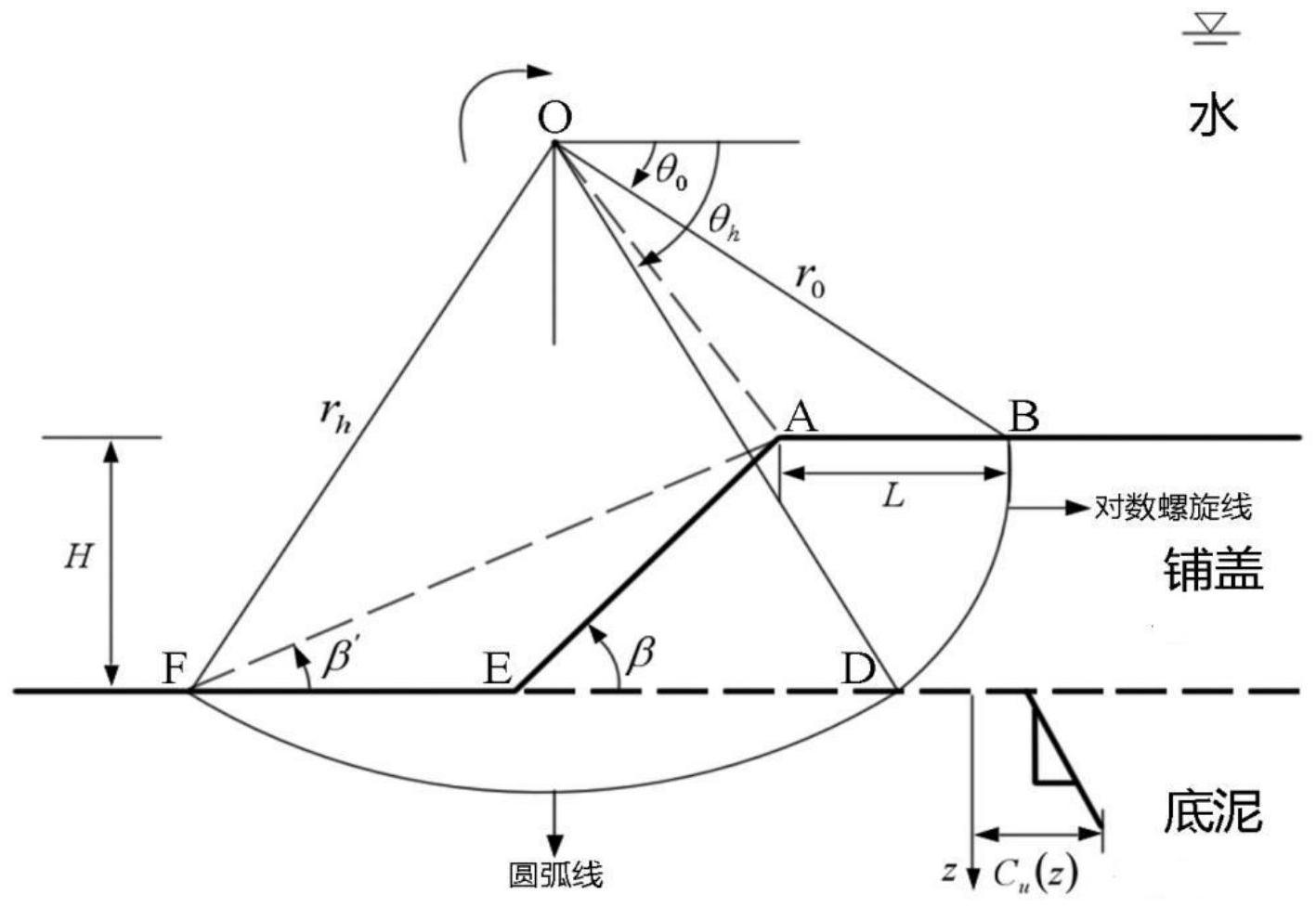
基于此，提供一种覆盖底泥的铺盖临界失稳厚度的计算方法，精确计算铺盖底泥 的失稳厚度。 一种覆盖底泥的铺盖临界失稳厚度的计算方法，包括如下步骤： 建立铺盖临界失稳厚度计算模型； 利用气体溶解度算法求解所述铺盖临界失稳厚度计算模型，得到铺盖临界失稳厚 度。 以下还提供了若干可选方式，但并不作为对上述总体方案的额外限定，仅仅是进 一步的增补或优选，在没有技术或逻辑矛盾的前提下，各可选方式可单独针对上述总体方 案进行组合，还可以是多个可选方式之间进行组合。 可选的，铺盖的失稳破坏截面为对数螺旋线，底泥的失稳破坏截面为圆弧线，滑动 体重力所做的功等于失稳破坏面上内能的耗散率，所述铺盖临界失稳厚度计算模型的公式 如下： 7 CN 111597695 A 说　明　书 2/12 页 式中：Hcr为铺盖的临界失稳厚度； Cu0为底泥表面的抗剪强度； γ1为铺盖的饱和重度； 为铺盖的内摩擦角； θ0为对数螺旋线的起始角； θh为圆弧线的起始角； β′为圆弧线终点与铺盖坡顶点连线与水平面的夹角； β为铺盖坡脚； H为铺盖厚度； L为铺盖坡顶点与对数螺旋线起点的距离； r0为对数螺旋线和圆弧线的公共圆心到对数螺旋线起点的距离； f1,f3,f4,f5分别为计算滑动体重力所做功的函数； q1,q2分别为计算失稳破坏面上内能耗散率的函数。 可选的， 分别为角度θ0,θh,β′的函数，表达式如下： 式中： H为铺盖厚度； L为铺盖坡顶点与对数螺旋线起点的距离； r0为对数螺旋线和圆弧线的公共圆心到对数螺旋线起点的距离；Fs表示铺盖的稳 定系数； 为铺盖的内摩擦角； θ0为对数螺旋线的起始角； θh为圆弧线的起始角； 8 CN 111597695 A 说　明　书 3/12 页 β′为圆弧线终点与铺盖坡顶点的连线与水平面的夹角。 可选的，f1、f3、f4、f5的表达式分别如下： 式中： 为铺盖的内摩擦角； Fs表示铺盖的稳定系数； θh为圆弧线的起始角； θ0为对数螺旋线的起始角； L为铺盖坡顶点与对数螺旋线起点的距离； r0为对数螺旋线和圆弧线的公共圆心到对数螺旋线起点的距离；H为铺盖厚度； β′为圆弧线终点与铺盖坡顶点的连线与水平面的夹角； β为铺盖坡脚。 可选的，q1、q2的公式分别如下： 式中：c1为铺盖的粘聚力； Cu0为底泥表面的抗剪强度； ρ为底泥的抗剪强度随深度增大的速率； 为铺盖的内摩擦角； Fs表示铺盖的稳定系数； θh为圆弧线的起始角； θ0为对数螺旋线的起始角； 9 CN 111597695 A 说　明　书 4/12 页 r0为对数螺旋线和圆弧线的公共圆心到对数螺旋线起点的距离； H为铺盖厚度。 可选的，利用气体溶解度算法求解所述铺盖临界失稳厚度计算模型，包括： 步骤1，利用下式对气体位置进行初始化： Xi(t 1)＝Xmin r·(Xmax-Xmin) 式中：Xi为第i种气体的位置，铺盖模型中每组θ0,θh,β′对应一个气体位置Xi； t为当前迭代次数； r为0～1之间的随机数； Xmax,Xmin分别为气体的上限和下限位置； 步骤2，对各气体进行聚类，将相似气体划分至同一个簇，第i种气体在第j簇中的 亨利系数j(Hj(t))、分压Pi,j、溶解焓j(Ci)的表达式分别如下： j(Hi(t))＝l1×rand(0,1) ,Pi,j＝l2×rand(0,1) ,j(Ci)＝l3×rand(0,1) 式中：l1,l2,l3为常数，分别取0.05，100，0.01； 步骤3，对每个簇内的气体进行评价，根据评价结果对同个簇内的气体位置进行优 劣排序； 步骤4，根据气体位置的优劣排序，更新亨利系数、溶解度、以及各簇的气体位置； 步骤5，跳出局部极值； 步骤6，更新最差气体位置； 步骤7，重复步骤1～6，直至获得最佳气体位置即为铺盖临界失稳厚度。可选的，步 骤4中，依据下式对亨利系数进行更新： j(Hi(t 1))＝j(Hi(t))·exp(-j(Ci)·(1/T(t)-1/Tθ)) ,T(t)＝exp(-t/iter)式 中：j(Hi(t))为第t次迭代时簇j中的第i个气体的亨利系数； j(Ci)为簇j中的第i个气体的溶解焓； t为当前迭代次数； T是温度； Tθ为常数取298.15； iter为总迭代次数； 步骤4中，依据下式对溶解度进行更新： Si,j(t 1)＝K·j(Hi(t))·Pi,j(t) 式中：Si,j,Pi,j分别为第i种气体在第j簇中的溶解度和分压； j(Hi(t))为第t次迭代时簇j中的第i个气体的亨利系数； t为当前迭代次数； K为常数； 步骤4中，依据下式对气体位置进行更新： Xi ,j(t 1)＝Xi ,j(t) F·r·γ·(Xi ,best(t)-Xi ,j(t)) F·r·α·(Si ,j(t)·Xbest (t)-Xi,j(t)) 式中：Xi,j为第i种气体在第j簇中的位置； 10 CN 111597695 A 说　明　书 5/12 页 r为随机数； t为当前迭代次数； Xi,best为第i种气体在第j簇中的最优气体位置； Xbest为全局最优气体位置； γ表示j簇中第i种气体与簇中其他气体相互作用的能力； α表示j簇中其他气体对第i种气体的影响，值为1； β为常数； Fi,j表示第i种气体在第j簇中的适应度值； Si,j为第i种气体在第j簇中的溶解度； Fbest表示全局最优适应度值； F为符号函数，通过正负值来改变搜索方向。 可选的，步骤5中，依据下式跳出局部极值： Nw＝N·(rand(c2-c1) c1) ,c1＝0.1and  c2＝0.2 式中：Nw为最差的气体个数； N为气体总数。 可选的，步骤6中，依据下式更新最差气体： G(i,j)＝Gmin(i,j) r·(Gmax(i,j)-Gmin(i,j)) 式中：G(i,j)表示第i种气体在第j簇中的位置； r为随机数； Gmax(i,j) ,Gmin(i,j)分别为第i种气体在第j簇中的位置的最大值和最小值。 本申请还提供了一种覆盖底泥的铺盖临界失稳厚度的计算系统，包括： 第一模块，用于建立铺盖临界失稳厚度计算模型； 第二模块，用于利用气体溶解度算法求解所述铺盖临界失稳厚度计算模型，得到 铺盖临界失稳厚度。 本申请提供的铺盖临界失稳厚度计算方法，可以快速求解得到铺盖临界失稳厚 度，为铺盖的厚度设计提供依据。 附图说明 图1为本申请中铺盖临界失稳厚度计算模型的各符号含义示意图； 图2为利用气体溶解度算法求解铺盖临界失稳厚度计算模型的流程图； 图3为软土地基中抗剪强度随深度的变化曲线； 图4为10次迭代计算的平均最优适应度函数值随迭代次数的变化曲线。