技术摘要：
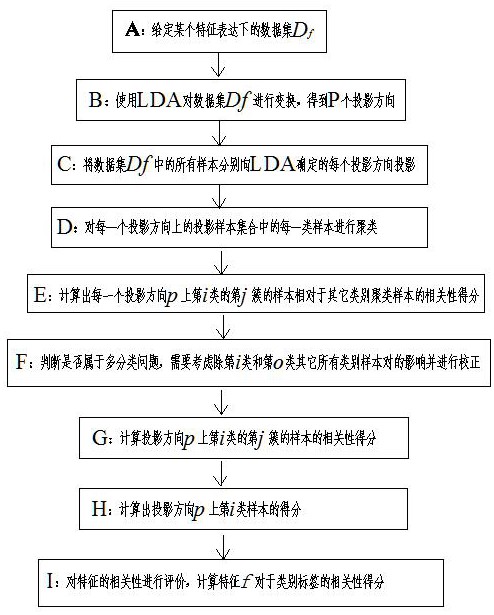
本发明公开了一种基于局部线性判别分析的特征相关性评价方法，包括以下步骤：A：设给定某个特征f表达下的数据集；B：使用LDA对数据集进行变换得到P个投影方向；C：将数据集中的所有样本分别向LDA确定的每个投影方向投影；D：对每一个投影方向上的投影样本集合中的每一  全部
背景技术：
特征相关性评估是机器学习领域特征选择技术中的关键技术，其作用是评估特征 与标签之间的关联程度，从而为特征选择提供特征重要性评价。线性判别分析(Linear  Discriminant  Analysis,LDA)是一种经典的线性学习方法，主要原理是将高维数据根据标 签信息有监督的投影到低维空间，其投影方向需要满足使得同类样本的投影点尽可能相互 接近、异类样本的投影点尽可能相互远离，即费舍尔距离最大，从而使样本在该空间具有最 佳的可分离性。LDA可以用于分类任务下特征相关性的评价，即将特征数据进行LDA变换，在 各LDA投影方向上费舍尔距离越大的特征，其特征相关性越大(特征可分性越强)。在样本服 从高斯分布下，LDA对特征相关性的评价效果较好。然而在实际中，样本往往不服从理想高 斯分布，此时使用LDA对特征进行相关性评价的效果较差。
技术实现要素：
本发明的目的是提供一种基于局部线性判别分析的特征相关性评价方法，能够有 效避免LDA对非高斯数据特征进行相关性评价时不准确的问题。 本发明采用下述技术方案： 一种基于局部线性判别分析的特征相关性评价方法，依次包括以下步骤： A：设给定某个特征f表达下的数据集 ym∈{1 ,2 ,...,K}，其 中， 是特征f表达下的第m个数据样本，ym是第m个数据样本的标签，K为类别数，K≥ 2，d是特征维度，M是样本数目； B：使用LDA对数据集Df进行变换，得到P个投影方向wp，p＝1,2,…,P，其中P＝min {K-1,d}； C：将数据集Df中的所有样本分别向LDA确定的每个投影方向投影，第p个投影方向 的投影样本集合记为 D：对每一个投影方向上的投影样本集合 中的每一类样本进行聚类，在第p个投 影方向上的第i类聚类样本记为 样本数记为 i∈{1,2,...,K}； 聚类后形成的簇 的数目记为 的第j簇的样本记为 的样本数目记为 E：计算出每一个投影方向p上第i类的第j簇的样本 相对于其它类别聚类样本 的相关性得分 4 CN 111738334 A 说　明　书 2/6 页 其中，o∈{1,2,...,K}，o≠i， 表示投影方向p上第o类的第l簇， 表示 的 簇的数目， 表示 的样本数目， 表示 的样本数目， 表示 和 的LDA得分； 其中，λ是矩阵 Sb的特征值，Sω和Sb分别是LDA变换中的类内散度矩阵和类间散 度矩阵； F：判断K是否大于2，若K>2，对 进行校正： 设除了第i类和第o类之外类别q的聚类样本 的簇的样本区间与簇 的样本 区间重叠，并将簇 的样本区间分成了 个区间，q∈{1,2,...,K}，q≠i且q≠o；第t 个区间内除了第i类和第o类之外类别q的聚类样本为干扰样本，干扰样本的数目为 第t个区间内 的样本数目为 则校正后的相关性得 分 为 G：计算 的相关性得分 H：计算出投影方向p上第i类样本的得分 I：对特征f的相关性进行评价，计算特征f对于类别标签Y＝[y1 ,y2,...,ym]T的相 关性得分Sf： 5 CN 111738334 A 说　明　书 3/6 页 其中，Np是所有类别在p方向的聚类样本数目。 所述的步骤D中，采用基于密度的对噪声鲁棒的空间聚类算法分别对投影样本集 合 中的每一类样本进行聚类。 本发明首先利用LDA变换得到与分类相关的全局最佳投影方向，然后在每个投影 方向上对投影样本点进行局部特征评价。利用聚类的思想寻找样本分布的多个簇，化整为 零，以每个投影方向下的每个类别的每个簇为基本单位进行LDA特征评价得分，然后通过一 系列得分加权求和最终得到对该特征数据的相关性评价得分，能够有效避免LDA对非高斯 数据特征进行相关性评价时不准确的问题。 附图说明 图1为本发明的流程示意图； 图2为实施例1中局部LDA特征相关性得分校正示意图。