技术摘要：
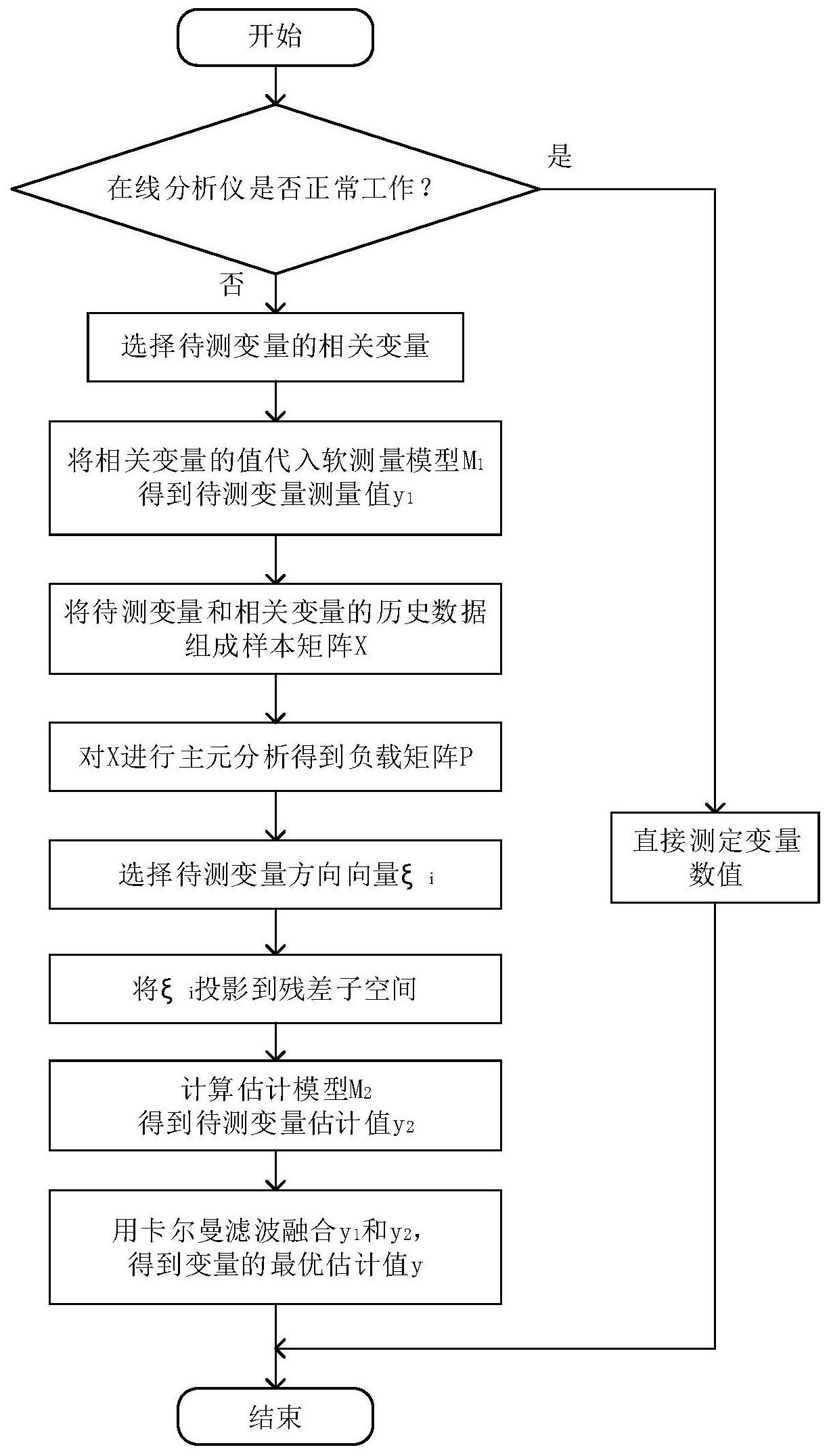
本发明公开了一种常压塔顶油干点在线分析检测方法，该方法首先判断在线分析仪能否正常工作，若无法工作则根据工艺机理选择相关变量，然后通过软测量模型M1计算塔顶油干点测量值y1；再对待测变量和相关变量的历史数据进行主元分析，得到估计模型M2，计算塔顶油干点估计  全部
背景技术：
在原油蒸馏过程的先进控制中，经常会使用以质量指标为被控参数的多变量控 制，从而达到产品收率最高、装置的加工能耗最小、同时又保证产品质量卡边的目的，使经 济效益最大化。其中，常顶油干点是常顶产品的主要质量控制指标。 常顶油干点很难用仪表直接测得，多数依赖于离线分析化验，实时性差，无法实现 质量闭环控制。后来出现了基于近红外光谱的在线分析技术，将常顶油取样换热到40℃后 分析光谱数据从而计算干点，但近红外光谱仪成本高，有时会产生故障或处于维护状态。基 于软测量技术计算干点可基于机理模型或统计模型。机理模型以物理和化学等科学原理为 基础，运用物料平衡、能量平衡等技术，获得常顶油干点与相关过程变量的数学模型，但机 理模型的建立需要对原油蒸馏过程有深刻的认识，并且伴随着一些假设条件，因此模型精 度不够高。统计模型是采集相当多的过程历史数据，运用统计分析数据处理方法建模，但由 于原油性质及操作工况经常发生变化，造成所建模型的实际计算精度降低。
技术实现要素：
针对上述问题，本发明公开一种常压塔顶油干点在线分析检测方法，通过选择相 关变量，基于主元分析建立估计模型，并将常顶油干点估计值与通过软测量模型得到的测 量值融合，得到最优估计值，从而实现常顶油干点的在线检测。 本方法具有以下步骤： (1)判断常顶油干点在线分析仪是否工作正常，若正常，则直接测定干点值，转步 骤(9)，若无法工作，则转步骤(2)； (2)选择与待测变量相关的变量组成向量x； (3)通过软测量计算得到系统的状态空间模型M1，算出待测变量的测量值y1； (4)取待测变量和相关变量的正常历史数据作为训练集，组成样本矩阵X； (5)对样本矩阵X进行主元分析，得到负载矩阵P； (6)令待测变量的方向向量ξi＝[1  0  …  0]T，并计算ξi向残差子空间的投影 (7)计算估计模型M2： y2＝Cx                                 (2) 3 CN 111592907 A 说　明　书 2/5 页 其中，y2为待测变量的估计值，I1为单位矩阵， 为单位化后的 I2为比I1少一维 的单位矩阵； (8)采用卡尔曼滤波融合测量值y1和估计值y2，得到变量的最优估计值y； (9)结束。 本方法中，选择与塔顶油干点相关的变量包括：常压塔塔顶温度、常压塔塔顶压 力、常压塔塔顶冷回流温度、常压塔中间层气相温度、常压塔进料温度、顶循回流取热比、一 中回流取热比，共7个变量。 本方法中，顶循回流取热比P1可以由常压塔顶循回流流量F1、常压塔常顶循换热温 度差ΔT1和进料量F计算得到： 本方法中，一中回流取热比P2可以由常一中回流流量F2、常压塔常一中换热温度差 ΔT2和进料量F计算得到： 本方法中，模型M1可以由机理分析法结合最小二乘回归得到。 有益效果： 本发明公开的常压塔顶油干点在线分析检测方法，能够当在线分析仪无法工作 时，根据其它已测量的相关变量，使用基于主元分析的估计模型通过变量间的相关关系估 计出塔顶油干点，并且与软测量计算得到的测量值进行综合计算，得到最优估计值，使结果 更加准确，有利于工业过程的先进控制工程有效实施，提高企业经济效益。 附图说明 图1是常压塔顶油干点在线分析检测方法的实施流程图 图2是某炼油企业常压塔的工艺示意图 图3是某炼油企业常压塔塔顶油干点在线分析检测结果对比图 具体实施过程 下面结合附图以及具体的算例，给出详细的计算过程和具体操作流程，以对本发 明作进一步说明。本实施案例在以本发明技术方案为前提下进行实施，但本发明的保护范 围不限于下述的实施案例。 本案例以某炼油企业为例，为保证生产过程平稳运行，并且在保证产品质量的同 时降低成本，该企业为原油常减压蒸馏装置设计了多个先进控制器，包括炉效率控制器、常 压炉支路平衡控制器、常压塔控制器等。其中常顶油干点是常顶产品的主要质量控制指标， 是常压塔控制器中一个重要的被控变量。 下面以该企业常减压装置中常压塔塔顶油干点的在线分析检测来说明本方法的 有效性及实施过程。选定500组数据，其中前400组作为训练集，后100组作为测试集对本方 法进行验证。本案例实施流程如图1所示，具体的实施步骤如下： 首先，从工艺机理出发，定性分析与常顶油干点相关的因素，该企业常压塔的工艺 4 CN 111592907 A 说　明　书 3/5 页 示意图如图2所示。根据具体工艺分析，常顶油干点与常压塔塔顶温度、常压塔塔顶压力、常 压塔塔顶冷回流温度、常压塔中间层气相温度(本案例中取常压塔35层气相温度)、常压塔 进料温度、一中回流取热比、顶循回流取热比共7个变量有关，如表1所示： 表1常压塔塔顶产品干点相关变量 序号 DCS位号 变量描述 1 TI1103A.PV 常压塔塔顶温度 2 PI1112.PV 常压塔塔顶压力 3 TI1135.PV 常压塔塔顶冷回流温度 4 TI1129.PV 常压塔35层气相温度 5 TI1139.PV 常压塔进料温度 6 T2LOOP1.PV 顶循回流取热比 7 T2LOOP2.PV 一中回流取热比 其中一中回流取热比和顶循回流取热比可以使用换热温度差、流量和进料量计算 得到，公式如表2所示： 表2中间变量计算公式 通过机理分析结合偏最小二乘法建立常顶油干点软测量模型M1，写成空间状态系 统模型形式如下： x(t)＝Ax(t-1)                                (1) y1(t)＝Bx(t)                                 (2) 其中x(t)为t时刻的状态矢量，为7×1的向量，由上述7个相关变量组成；状态转移 5 CN 111592907 A 说　明　书 4/5 页 矩阵 y1(t)为t时刻的常顶油干点测量值； 状态观测矩阵B＝[1.0129  0.5134  0.5967  …  0.9265]。 将测试集中100组数据均代入软测量模型M1计算，得到常顶油干点的测量结果如 图3a所示，均方误差MSE1＝3.5360，最大误差为6.0544。 然后将训练集中400组样本组成训练矩阵X，进行主元分析，得到的主元个数为6， 负载矩阵P维数为8×6，具体如式(3)所示： 将100组测试集数据组成测试矩阵，令待测变量的方向向量ξ＝[1  0  0  …  0]Ti ，将 负载矩阵P代入计算ξi向残差子空间的投影 如式(4)所示： 计算模型M2，如式(5)、(6)所示： y2＝Cx                                 (5) 按照模型M2计算得到待测变量值y2，如图3b所示，均方误差MSE2＝2.6731，最大误 差为4.8317。 将y1(t)和y2(t)按照如式(7)～(12)所示的卡尔曼滤波公式进行迭代计算： x(t|t-1)＝Ax(t-1)                             (7) P(t|t-1)＝AP(t-1)AT                           (8) K(t)＝P(t|t-1)CT[CP(t|t-1)CT]-1                     (9) x(t)＝x(t|t-1) K(t)(y(t)-Cx(t|t-1))                   (10) y(t)＝Cx(t)                               (11) P(t)＝(I-K(t)C)P(t|t-1)                        (12) 其中矩阵A、C分别为模型M1、M2的参数矩阵，在上述步骤中已计算得出；令初始值y (0)＝170，P(0)为所有元素为0.1的7×7维矩阵；x(t|t-1)为基于t-1时刻的状态矢量x(t- 1)根据模型M1递推得到的t时刻状态矢量值；P(t|t-1)为x(t|t-1)对应的状态矢量协方差 6 CN 111592907 A 说　明　书 5/5 页 矩阵；P(t)为x(t)对应的协方差矩阵；K(t)为t时刻的卡尔曼增益矩阵；x(t)为t时刻状态矢 量的最优估计；y(t)为t时刻常顶油干点的最优估计。 卡尔曼滤波后最终得到常顶油干点的最优估计值，如图3c所示，均方误差MSE3＝ 1.0526，最大误差为3.3645。 上述三种结果的误差比较如表3所示，本方法的均方误差和最大误差比模型M1和M2 的结果都要小，因此本方法能更准确地得到待测变量值，满足工艺控制要求。 表3误差比较 模型 均方误差 最大误差 M1 3.5360 6.0544 M2 2.6731 4.8317 融合值 1.0526 3.3645 7 CN 111592907 A 说　明　书　附　图 1/3 页 图1 8 CN 111592907 A 说　明　书　附　图 2/3 页 图2 9 CN 111592907 A 说　明　书　附　图 3/3 页 图3 10