技术摘要：
本申请公开了一种针对SISO及MIMO系统的有界性PID控制算法，包括两个核心部分：单路或者多路带积分反馈的PID控制单元、和单输出或者多输出有界控制单元；并且单输出或者多输出有界控制单元将一个时变控制参数k0反馈到单路或者多路带积分反馈的PID控制单元中。本申请增强  全部
背景技术：
PID控制算法起源于20世纪20至30年代。PID即：Proportional(比例)、  Integral (积分)、Differential(微分)的缩写。现今，PID控制算法是自动控制系统中非常广泛应用 的一种控制算法，比如在机械系统、电气系统、液压系统、或者各种复合系统等工业控制系 统中控制目标的调节，都可以使用PID控制算法。其具有结构简单、稳定性好、适用面广、工 作可靠、调整方便等优点。 尽管PID控制算法有很多的优点及广泛的应用，该控制算法也存在一定的缺陷。比 如，在绝大多数控制系统中，执行器或者执行机构都有着边界的要求，这与执行器的物理特 性相关，或者被控对象的物理特性或者安全特性相关。一旦执行器有边界性要求，往往会造 成PID控制算法的积分饱和(integral  windup)或者积分失控现象。该现象的主要原因是， 如果PID的输入误差有大幅度变化，积分器因为大幅度变化的误差的导致很大的累计量，并 且执行器已经达到了控制边界，而无法及时响应PID控制器输出。该累计误差往往会造成 PID无法对控制对象准确而可靠的控制，甚至会导致整个控制系统的不稳定。 尽管目前有一定方法来处理PID控制的饱和问题，比如抗饱和(Anti-windup)  方 法，智能积分管理，或者积分累计量上下限设计等等，但是这行方法在系统稳定性、复杂程 度或者控制响应上都存在或多或少的缺陷。并且这些方法都不太适合于MIMO系统的PID控 制算法。
技术实现要素：
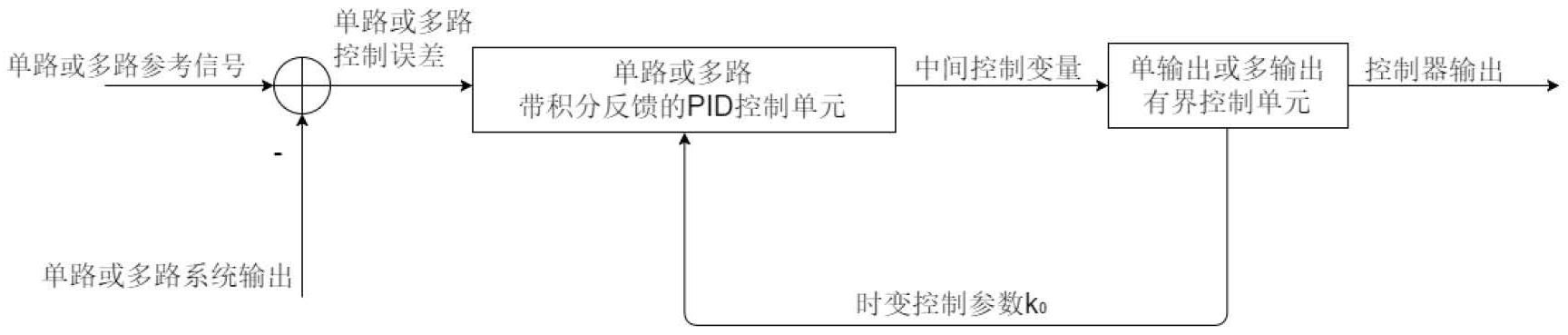
为解决现有PID算法中的技术不足，本发明提出一种针对SISO(单输入单输出)及 MIMO(多输入多输出)系统有界性PID控制算法，用于避免传统的积分饱和或者积分失控现 象。该有界性PID控制算法既可以应用于SISO系统，也可以拓展到MIMO系统。 针对SISO及MIMO系统的有界性PID控制算法，包括：单路或多路带积分反馈的PID 控制单元和单输出或多输出有界控制单元； 其中，单路带积分反馈的PID控制单元和单输出有界控制单元针对SISO系统，多路 带积分反馈的PID控制单元和多输出有界控制单元针对MIMO系统； 所述的针对SISO及MIMO系统的有界性PID控制算法，将单路或者多路参考信号与 单路或者多路系统输出作差得到单路或者多路控制误差，然后将该控制误差输入到单路或 者多路带积分反馈的PID控制单元；所述单路或者多路带积分反馈的PID控制单元的输出又 与单输出或者多输出有界控制单元相连接；所述单输出或者多输出有界性控制单元的最终 输出为所述有界性PID控制算法的最终输出；并且所述单输出或者多输出有界控制单元将 一个时变控制参数k0反馈到单路或者多路带积分反馈的PID控制单元中。 5 CN 111610712 A 说　明　书 2/11 页 其中SISO系统的有界问题为u∈(umin,umax)问题，u为控制算法的最终输出或者执 行器(执行机构)的控制输入,umax和umin分别为控制算法最终输出或者执行器(执行机构)控 制输入的 上界 (极大值) 与下界 (极小值) 。其中 M I M I O  系统的 有界问 题为 问题，ui为多路控制算法的最终输出或者多路执行器(执行机构)的 控制输入，umax＞0为多路控制算法输出正交矢量和的上界。 针对SISO系统的有界性PID控制算法，包括两个核心部分：单路带积分反馈的PID 控制单元和单输出有界控制单元； 为解决u∈(umin,umax)有界和积分饱和问题，该针对SISO系统的有界性PID  控制算 法，将单路参考信号与单路系统输出作差得到单路控制误差，然后将该控制误差输入到单 路带积分反馈的PID控制单元；所述单路带积分反馈的PID控制单元的输出又与单输出有界 控制单元相连接；所述单输出有界性控制单元的最终输出为所述针对SISO系统的有界性 PID控制算法的最终输出，并且所述单输出有界控制单元将时变控制参数k0反馈到单路带 积分反馈的PID控制单元中。 其中，所述单路带积分反馈的PID控制单元，包括：比例单元、微分单元和带反馈的 积分单元； 所述单路带积分反馈的PID控制单元接收单路参考信号与单路系统输出作差得到 的单路控制误差，所述单路控制误差分别输入到所述单路带积分反馈的PID控制单元的比 例单元、微分单元、和带反馈的积分单元，然后将所述比例单元、微分单元、带反馈的积分单 元的输出相加，即得到所述单路带积分反馈的  PID控制单元的输出。 所述比例单元为：KPE，其中，KP为比例系数，E为参考信号与系统输出之差得到的误 差； 所述微分单元为： 其中，KD为微分系数， 为误差的微分； 所述带反馈的积分单元为：k0KI∫Edt，其中，k0为从所述有界控制单元中反馈回来 的时变控制参数，k0∈(0,1]，KI为积分系数，∫Edt为对误差的积分； 所述单路带积分反馈的PID控制单元表示为： 其中，um是所述单路带积分反馈的PID控制单元的输出，为一个中间控制变量，可 将其输入到单输出有界控制单元中。 所述单输出有界控制单元，用于接收所述单路带积分反馈的PID控制单元的输出， 然后输出所述针对SISO系统的有界性PID控制算法的最终输出，并且将时变控制参数k0反 馈到单路带积分反馈的PID控制单元中； 所述单输出有界控制单元表示为： 6 CN 111610712 A 说　明　书 3/11 页 其中，u既是单输出有界控制单元的输出，也是整个所述针对SISO系统的有界性 PID控制算法的最终输出。um来源于所述单路带积分反馈的PID控制单元；umax和umin为所述 有界性PID控制算法控制输出的极大值与极小值。k为一个可以调整的定值控制参数，且k＞ 0，k1也为一个可以调整的定值控制参数，且k1＞0，k0为一个时变控制参数，将进一步反馈到 单路带积分反馈的PID控制单元中，且k0∈(0,1]。 给出u与k0关系为： 该方程为一个椭圆方程。其中，通过有界控制单元的上述公式(2)与(3)和李雅普 诺夫稳定性分析方法,可以证明u与k0关系的公式是正确的，李雅普诺夫分析过程详见具体 实施方式。 通过该椭圆方程，可以轻易的得到所述针对SISO系统的有界性PID控制算法的最 终控制输出满足u∈(umin,umax)，从而保证所述有界性PID控制算法输出的有界性。然后通过 合理的初始点的选择，时变控制参数k0将保证在k0∈(0,1]范围以内。并且可以注意到，如果 所述针对SISO系统的有界性PID控制算法的最终控制输出已经趋近于极大值或者极小值， 即u→umin,或者u→umax，时变控制参数k0将趋近于0，即k0→0。然后通过k0对所述单路带积分 反馈的PID控制单元的积分项的反馈，使所述单路带积分反馈的PID控制单元的积分项也趋 近于0，即k0KI∫Edt→0，从而天然的避免了积分饱和或者积分失控现象。 上述所述针对SISO系统的有界性PID控制算法还可以拓展到MIMO系统中。针对 MIMO系统的有界性PID控制算法，也包括两个核心部分：多路带积分反馈的PID控制单元和 多输出有界控制单元； 为解决 有界和积分饱和问题，该针对MIMO系统的有界性 PID控制算法，将多路参考信号与多路系统输出作差得到多路控制误差，然后将所述多路控 制误差分别输入到多路带积分反馈的PID控制单元；所述多路带积分反馈的PID控制单元的 输出分别与一个统一的多输出有界控制单元相连接；所述多输出有界性控制单元具有多路 输出，所述多路输出即为所述针对  MIMO系统的有界性PID控制算法的最终输出，并且所述 多输出有界控制单元将一个时变控制参数k0分别反馈到多路带积分反馈的PID控制单元 中。 其中，每一路带积分反馈的PID单元可以表示成： 其中，i＝1,2,…,n，n为所述针对MIMO系统的有界性PID控制算法的总路数，该总 路数与MIMO系统本身的总路数有关，umi是第i路的中间控制变量，  KPi、KDi、KIi分别为比例控 7 CN 111610712 A 说　明　书 4/11 页 制参数、积分控制参数以及积分控制参数，Ei＝Ri-Yi为第i个误差信号。Ri为第i个参考信 号，Yi为第i个系统输出，k0为从有界控制单元中反馈过来的时变控制参数，k0∈(0,1]。 所述多输出有界控制单元，包含多路控制输出，其表示成： 其中，ui有界性控制单元的多路输出，也是整个所述针对MIMO系统的有界性PID控 制算法的最终输出。umi来源于所述多路带积分反馈的PID控制单元；umax＞0为多路控制算法 输出ui正交矢量和的上界。与所述针对SISO系统的有界性PID控制算法类似，k＞0为一个可 以调整的定值控制参数，ki＞0也为对应每路的可以调整的定值控制参数，k0∈(0,1]为一个 时变控制参数将从多输出有界控制单元中进一步反馈到所述的每一路带积分反馈的PID单 元。 通过该有界控制单元的设计和李雅普诺夫稳定性分析方法,可以得到ui与k0关系 为： 该论证过程详见