技术摘要：
数据时效性是反映数据时间特征的属性，对数据质量和价值有重要影响。数据的时间标记一旦丢失或篡改，很难进行绝对的精确修复。基于一些规律规则，修复数据相对时效，满足数据质量和数据挖掘对数据时序关系的需求是可行的。在数据时效规则相关研究基础上，对基本的时效  全部
背景技术：
大数据和人工智能时代,数据质量反映了数据的可用性和价值,是影响数据资产 价值的核心因素之一。数据质量的评价是个复杂的问题,涉及到主观、客观等众多影响因素 的多维度综合评估。一般来讲,数据的价值往往在数据挖掘、分析使用过程中得到更好的体 现,国内外学者更多倾向是从数据可用性角度认识与定义数据质量,Sargent将数据质量定 义为“使所有数据都能满足实际需求的能力”,Wang和Strong提出了“数据质量取决于这些 数据是否适用于上下文并适合数据使用者的想法”。丁小欧等针对影响数据质量的4个关键 性质完整性、精确性、一致性、时效性提出了综合评估框,确定了数据质量多维关联关系评 估策略,李建中等深入总结研究了数据可用性判定问题,在国内外相关研究基础上总结提 出一致性、精确性、完整性、时效性和实体同一性等5个实际可行的数据可用性度量指标,对 其中“时效性”的解释是“每个信息都与时俱进,不过时”,并且指出数据精确性和数据时效 性方面研究工作较少,亟需深入系统研究。 时效性是数据的重要属性,是数据有关时间的特征,反映了数据在其建模的世界 中“新”的程度,关系到数据质量、数据可用性和数据价值。在数据分析、数据挖掘和数据增 值应用中,如时间序列分析、流程挖掘、关联和推荐等算法中,数据时效的准确与否通常会 决定数据分析结果的可靠性和可用性,使用过期或者时间错乱的数据可能会做出错误的决 策。早在2002年,有专家报告指出,在商业和医疗领域,数据质量退化非常快,由于客户信息 的变化,每月至少有2％的数据因过时失效,并且经过测算,如果这些过时数据没有被有效 修复,在2年内会有近一半的数据记录因过时而不可用。面对纷繁芜杂的数据,如果无法确 定数据的新旧,无法判断数据是否过时,数据查询可能会返回错误的结果,分析挖掘可能会 得到相悖的结论,造成数据质量下降、可用性降低、生产要素地位被削弱和数据资产贬值。 数据时效的判定是改善提高数据质量的重要手段。在大数据和人工智能时代,人 们的各类数据非集中化地分布在各类平台和系统中,形成很多数据孤岛,无法进行统一管 理和更新、维护,数据时效不精确、数据过时带来的问题愈加严重。由于缺乏及时有效的维 护或数据集成融合等原因,很多数据的时间戳经常不可用或不精确，很难完全依赖精确的 时间戳进行数据的时效性判定。虽然时间戳有可能缺失或不精确,但是记录人们生产生活 的数据是有一定的规律性的。例如一个人不同时期两条记录,学位状态分别为“学士”和“硕 士”,即使没有时间戳,我们也可以确定“硕士”的记录要新一些,或者即便“学士”记录的时 间戳更新一些,我们几乎也可以判定是时间戳有误或数据异常。婚姻状态、年龄、薪酬等很 多属性都有类似的特征。通过在数据中学习和提取这些规律,虽然很难进行绝对的时效性 判定、还原数据精确的时间戳,但是我们可以进行相对时效的判定、修复记录的先后顺序, 判定数据的新旧,发现数据中的时效异常,提高数据时效质量和数据可用性,满足数据挖 6 CN 111581185 A 说　明　书 2/10 页 掘、创新应用的数据质量要求。 本发明研究了基于时效规则的数据相对时效修复和异常数据检测等问题,主要在 以下几方面取得了一些进展和成果: (1)对基本时效规则形式进行了扩展,进一步明确了时效规则相关概念和性质,扩 展后的时效规则可支持并行算法和增量更新； (2)提出了可并行的时效规则抽取算法,包括规则抽取,规则合并,增量更新算法； (3)提出了基于规则的数据相对时效修复方法,明确了有冲突与无冲突时效修复 两类问题,并分别建立了针对这两类问题的修复度量模型； (4)探讨了基于时效修复的异常数据检测方法,可以用于发现实体的异常行为,或 过程中的异常事件和流程； (5)在真实数据集上进行了相关实验,结果表明时效规则抽取并行算法是有效的, 数据相对时效修复是可用的,异常数据检测方法可以有效发现异常数据。
技术实现要素：
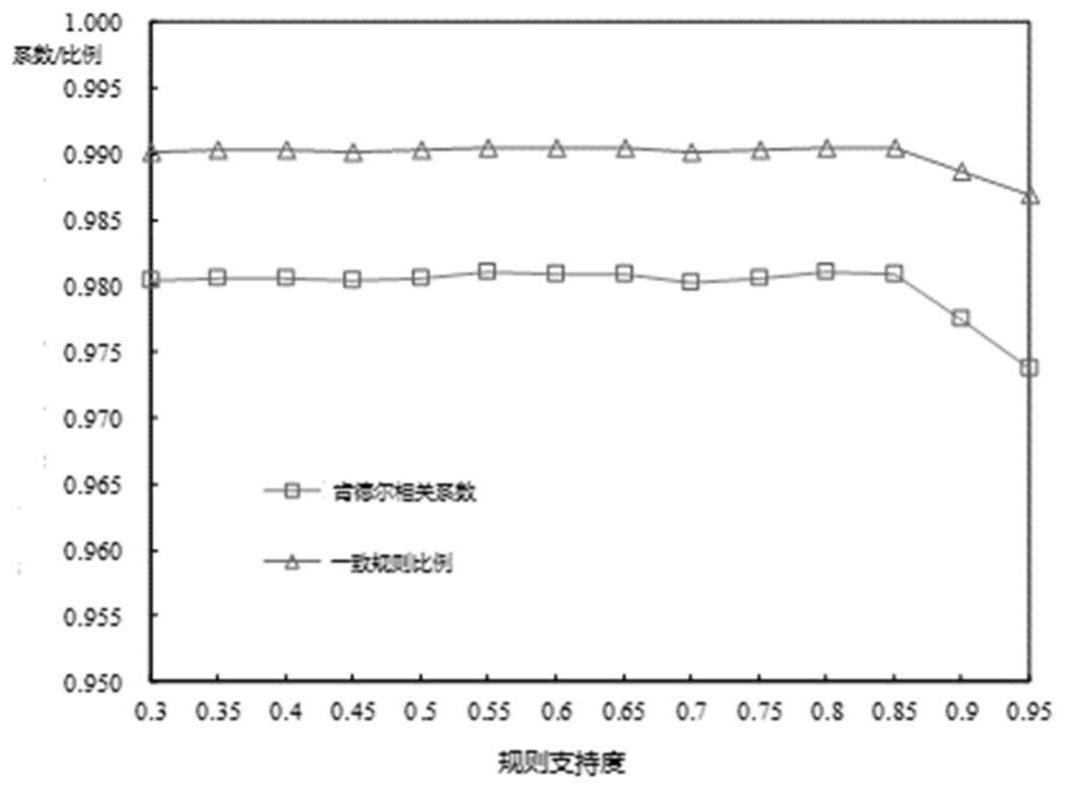
本发明旨在提出一种基于规则的数据相对时效修复与异常检测方法。 本发明解决其技术难题所采用的技术方案如下： 1)基本时效规则的扩展 在时效规则的定义中,每一条规则有一个支持度属性,其基本形式为:R(规则,支 持度)；这里的时效规则是一种二元规则，表示两个状态的先后顺序，支持度sr可以表示为： 对于某时效规则r,Sr表示支持度,O(r)为服从该规则的实体的集合,|O(r)|为服 从该规则的实体的数量,V(r) ,|V(r)|分别表示违背该规则的实体集合和违背该规则的实 体的数量，f(r)表示为强度函数,是一个表示服从该规则实体的频数的函数，如可选取 Logistic函数作为强度函数： 其中k是变化率,r0为平移常数,r＝r0时,f(r)函数值为0.5；如设置r0＝10,则服 从频数小于等于10时,f(r)函数值域为(0,0.5],服从频数大于10时,f(r)函数值域为(0.5, 1.0)； 为了实现规则的增量更新和算法的并行化、保留更多规则信息以利于时效修复和 数据质量评价,对基本时效规则形式进行了扩展,每一条规则保留了更多信息,扩展后的规 则形式为： R(规则,服从数,违背数,平均长度) 其中,服从数o为数据集中满足该规则的实体数，违背数v表示数据集中违背该规 则的实体数,平均长度len表示规则的状态节点经过的边的数量；扩展后的时效规则与原规 则是相容的,不影响原时效规则支持度的计算,且满足以下重要性质： 性质1规则的可加性：不同记录集扫描得到的两条相同规则,可以合并为一条规 则； 7 CN 111581185 A 说　明　书 3/10 页 R1(pre→post,o1,v1,len1) R2(pre→post,o2,v2,len2) R1 R2＝R(pre→post,o,v,len) 其中，pre和post表示规则中的两个状态，o＝o1 o2,v＝v1 v2, 规则的可加性是实现规则库增量更新和并行化计算的重要条件； 性质2规则的逆反性：某规则R(pre→post,o,v,len) ,其逆规则为R'(post→pre, v,o,-len)； 规则的逆反性可有效减少需要存储的规则数量，如规则a→b和规则b→a是可逆 的； 2)可并行的时效规则抽取算法 ·时效规则抽取算法 算法1时效规则抽取算法： 输入:包含多个实体的记录集,每个实体对应具有时间戳属性的多条记录,实体集 为E,在记录集的属性A上提取状态类型时效规则； 输出：形式为R(规则,服从数,违背数,平均长度)的时效规则集合CRS； 算法步骤： ①对于实体集E中每一个实体e，在记录集中选出实体e的所有元组按照时间戳升 序排序，并给每个元组设定一个排序序号，从1开始依次递增，时间戳相同的元组的排序序 号相同；N表示实体e的所有元组数目； ②对于实体e中的所有元组，如果第i个元组的排列序号小于第j个元组，则建立规 则R，R的名称为“Ti[A]→Tj[A]”,其中Ti[A]表示第i个元组的属性A的值，Tj[A]表示第j个元 组的属性A的值,i的取值范围是从1到N-1的整数,j的取值范围是从i 1到N的整数；R的服从 数为1，违背数为0，平局长度为第j个元组与第i个元组排序序号的差值；将规则R插入到集 合CRS中； ③规则R的插入：在集合CRS中，如果规则R已经存在，对规则R进行更新(算法3)；如 果规则R不存在但其逆规则存在，计算规则R的逆规则R′(算法2)，对规则R′进行更新(算法 3)；如果规则R以及它的逆规则R′都不存在，则直接添加规则R； ④将实体集E中每一个实体的所有元组都按照步骤②和③抽取规则并插入到集合 CRS中； 算法2计算逆规则算法 输入：时效规则R(pre→post,o,v,len) 输出：原规则的逆规则R'(pre'→post',o',v',len') 算法步骤：给pre'赋值为post，post'赋值为pre，o'赋值为v，v'赋值为o，len'赋值 为-len； 算法3时效规则更新算法 输入:更新前的时效规则集合CRS,根据规则R属性值对CRS进行更新； 输出:更新后的时效规则集合CRS； 算法步骤： ①从集合CRS中选出与规则R(pre→post ,o ,v ,len)名称相同的规则R1(pre→ 8 CN 111581185 A 说　明　书 4/10 页 post,o1,v1,len1)； ②给o1重新赋值为o1 o,v1重新赋值为v1 v,len1重新赋值为： len1＝((o1 v1)*len1 (o v)*len)/(o1 v1 o v)   (3) ③对规则R1的更新写入到集合CRS中； ·规则抽取算法的增量更新 算法4时效规则集合增量更新算法 输入：已有的时效规则集合CRS,新增的包含多个实体的数据记录集合IRS,新增的 实体集为E,在记录集的属性A上提取状态类型时效规则； 输出：更新后的时效规则集合CRS； 算法步骤： ①根据算法1，在记录集合IRS中抽取属性A的状态时效规则，记为ICRS； ②对于ICRS中的每一个规则R，将R插入到集合CRS中；如果规则R已经存在，对规则 R进行更新(算法3)；如果规则R不存在但其逆规则存在，计算规则R的逆规则R′(算法2)，对 规则R′进行更新(算法3)；如果规则R以及它的逆规则R′都不存在，则直接添加规则R； ·规则抽取算法的并行化 时效规则的提取,可以在多个节点上并行执行；首先对需要提取规则的数据集按 记录的实体进行分割(同一实体的记录尽量不分散到多个节点),多个结点上同时运行算法 1抽取时效规则集合,对抽取到的n个规则集合CRS1,CRS2,CRS3,…,CRSn,可以在单个结点或 多个结点上按一定策略执行算法4进行合并； 在对规则集进行合并时,可以采用两种合并策略： 第一种合并策略是在单个结点上非并行执行,依次将第2,3,…,n个规则集合并到 第1个规则集,第n个集合处理完成后,得到的第1个集合即为完备的规则集,无法并行执行, 时间复杂度为O(n-1)； 第二种策略合并规则集合分别在不同结点上完成,不同集合合并可以同时进行, 最后合并成一个完备的规则集合,时间复杂度为O(log(n))； 3)基于规则的数据相对时效修复与异常检测 ·数据时序修复 在一个数据记录集中，如果某实体的数据集时间标签丢失，可以通过提取其他实 体的状态时效规则，计算并修复丢失时间标签的数据集的数据相对时序； 算法5数据相对时效修复算法 输入:已提取的时效规则集合CRS,待修复记录时序的实体e的缺失时效标签的数 据集T,指定的时效属性A； 输出:修复完成的按相对时序排列的实体e的记录集合T′； 算法步骤： ①记集合T中的元组数目为n，从第一个元组开始，计算每个元组的属性A的值作为 规则名称中左边部分的所有规则路径长度之和； ②路径长度之和的计算：对于第i个元组，其路径长度之和Li初始为0，依次选择第 1,2,…,i-1,i 1,…,n个元组的属性A的值作为规则名称的右边部分，更新路径长度之和； 假如选择到了第j个元组，则组成的规则名称为’Ti[A]→Tj[A]’,如果该规则及其逆规则不 9 CN 111581185 A 说　明　书 5/10 页 存在于集合CRS中，Li的值不变，如果该规则或其逆规则存在于集合CRS中且平均长度和支 持度分别为len(r)和sr，则Li更新为： Li＝Li len(r)*sr   (4) 其中，支持度sr由公式(1)计算得到； ③当计算得到每个元组的属性A的值作为规则名称左边部分的所有路径长度之和 后，按照路径长度之和降序对元组排序，排序后的元组即为按照相对时序排列的数据集； ·有冲突与无冲突时效修复 无冲突时序修复，是指某实体待修复的记录本质上是按时间标签严格递增或递减 的序列，由于某种原因造成时间标记不准确或者缺失，顺序错乱，需要进行时序修复； 有冲突时序修复，是指某实体待修复的记录本质上是并非是按时间标签严格递增 或递减的序列，有一部分记录的状态的值是相同的，顺序错乱，需要进行时序修复； 针对这两类数据时效修复问题，分别引用或定义一些修复度量标准，用作评价修 复算法有效性的模型； 模型1肯德尔相关系数 使用τA对无冲突时序修复效果进行评价： 其中,其中nc表示两个随机变量中拥有一致性的顺序元素对的个数；nd表示不一致 性的元素对的个数,n0为所有的二元顺序对的个数； 模型2一致规则比例 适用于无冲突和有冲突时序修复；考虑两个可能存在相同元素的、有序的随机变 量X和Y,nX表示随机变量X的二元顺序对的个数，nc表示两个随机变量中拥有一致性的元素 对数，一致规则比例表示为： 模型3分段正确率 适用于有冲突时序修复评价；元素个数为n,每一部分重复元素划分为一个区间 段，一共有ns个区间,修复后序列按对应区间段统计相应元素落入这个区间段的个数,第i 个区间的正确元素个数为nci,最后统计所有划分到正确区间的元素所占比例： ·基于时效修复的异常数据检测 对于待检测的实体集E中的每一个实体e,判断实体e的数据记录是否存在异常的 检测过程如下： ①检索e的所有数据记录，按时间标签升序排列，时间缺失的记录可置于最先或最 后，得到序列S1； ②对序列S1进行随机乱序,然后基于时效规则,对其进行时序修复,得到修复后的 序列S2； ③根据序列S1判断是有冲突还是无冲突修复，根据修复类型选择合适的度量标 10 CN 111581185 A 说　明　书 6/10 页 准，计算修复前序列和修复后序列的时序相关性(度量模型值)，根据设定的阈值判定实体e 是否异常。 附图说明 图1规则提取算法的并行测试结果 图2时效规则集合的并行合并策略 图3规则合并算法的并行测试结果 图4无冲突时效修复两个模型的对比 图5有冲突时效修复两个模型的对比 图6两个模型的F1评分对比