技术摘要：
本发明提供的一种基于稳定广义有限元的弹性裂缝问题模拟方法，改进传统GFEM/XFEM的精度和条件数，使得裂缝问题的数值模拟更加精确和稳健，由于裂缝问题是结构分析技术的关键环节之一，因此本技术方案对工程力学中的结构分析领域有重要的促进作用。另外，本方法设计高度  全部
背景技术：
弹性裂缝和裂缝扩展模拟问题是力学问题中的一个重要问题，其相关性和重要性 源于数值断裂力学在飞机机身，压力容器，汽车零部件和铸件等安全关键零部件的疲劳寿 命预测中的广泛应用。疲劳破坏通常是由于表面或近表面裂缝的产生和传播而引起的，对 于任意形状的裂缝，只能采用数值方法来模拟裂缝扩展问题，裂缝问题数值模拟的主要环 节是弹性力学方程组的数值求解。 现有技术中，令Ω表达带裂缝ΓO和裂缝尖端O的裂缝区域，设Γ为Ω的边界，为 Γ的单位向外法向量。Γ由本质边界ΓD和自然边界ΓN组成，如图1所示。用粗体记号表达空 间中的矢量值函数或向量，例如u＝[u1，u T2] 。Ω内的裂缝问题的弹性方程组如下： 其中， 是应力张量，f是体力，g和u0分别是自然边界条件和本质边界条件， 是ΓO的单 位向外法向向量。x和y方向如图1所示，(r,θ)是对应的极坐标。 应变张量∈(u)记做 模型具体表示为： 其中前者是平面应变，而后者是平面应力，E是杨氏模量，v是泊松比。问题(P1)解u的主要部 6 CN 111597649 A 说　明　书 2/17 页 分对应于如下Ⅰ型和Ⅱ型开模型uI和uII[13,10]： 其中MI和MII是和压力强度因子有关的系数。E，v和κ是Kolosov常数([5,13,10])。u 在裂缝ΓO处是间断的，在裂缝尖O周围是奇异的。因此，常规有限元法(finite  element  method,FEM)在裂缝传播过程中需要不断地加密和更新网格，计算量极高。 针对这个困难，近二十年学者们发展了广义或扩展有限元方法(generalized/ extended  FEM,GFEM/XFEM)，该方法在固定规则网格FEM基础上增加富集函数(enrichment) 来求解裂缝问题，效率非常理想。GFEM/XFEM已广泛应用于各种工程问题，例如裂缝扩展，材 料建模，多相流和流体-结构相互作用等[2,7]。一些通用的有限元软件也已经将GFEM/XFEM 集成到框架之中，如Ansys，Abaqus，LS-dyna等。虽然GFEM/XFEM解决了网格计算量大的困 难，且达到比较高的计算精度，但是由于原有的有限元函数和新增加的富集函数之前存在 线性相关性，使得刚度矩阵的条件数很大，从而在求解线性方程组时可能导致显著的截断 误差，甚至可能导致数值模拟过程的失败。条件数问题已经成为GFEM/XFEM研究的主要技术 困难之一[4,7]，相关的研究工作很多[4,11,14,15]，但是目前为止尚未得到很好地解决。 此外，由于GFEM/XFEM的程序框架与通常的FEM有不同之处，跟FEM相比，GFEM/XFEM的并行化 处理和高性能计算方面也是一项挑战性的工作。
技术实现要素：
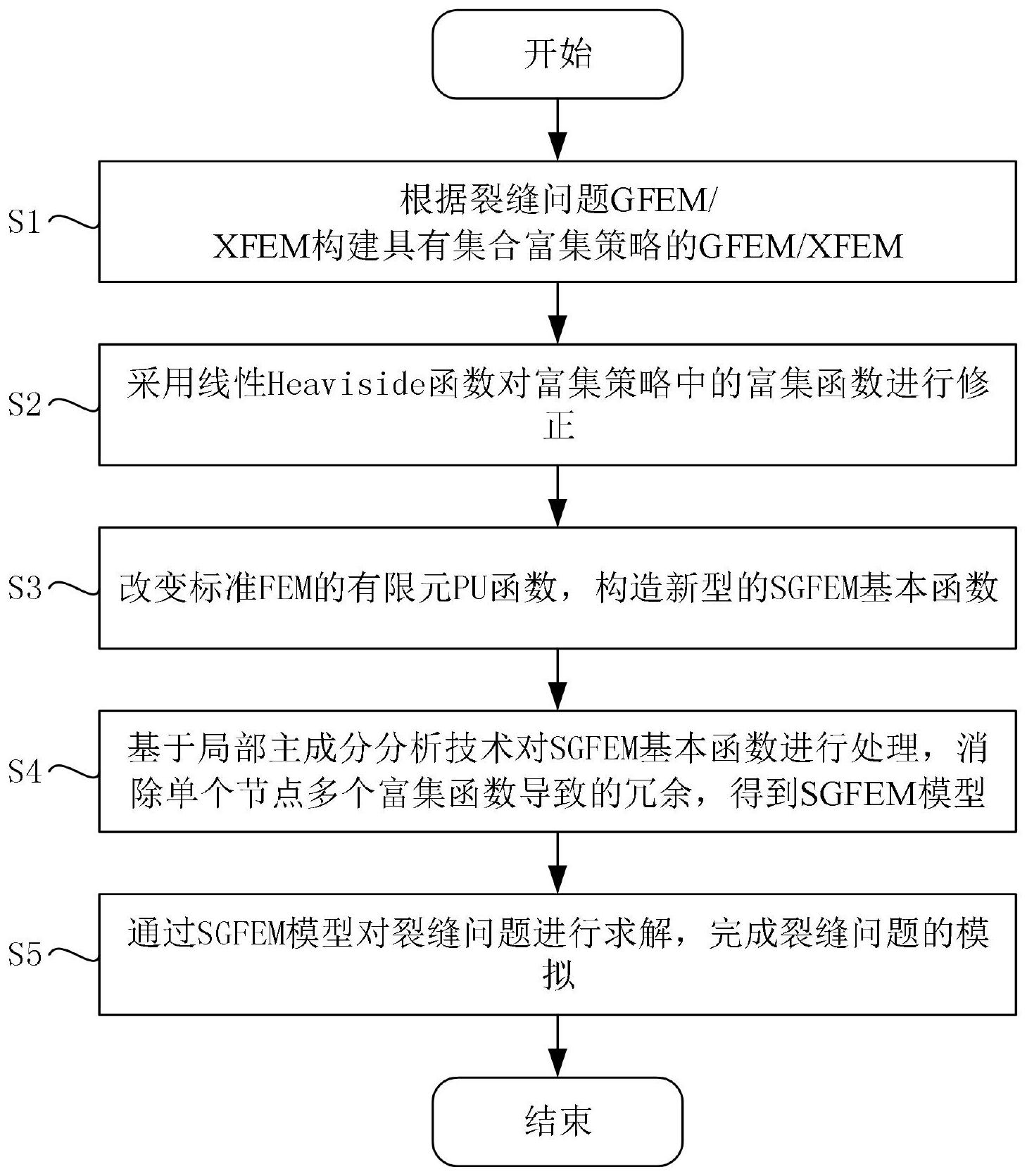
本发明为克服现有的广义或扩展有限元方法存在刚度矩阵的条件数很大，在求解 时存在可能导致显著的截断误差，甚至可能导致数值模拟过程的失败的技术缺陷，提供一 种基于稳定广义有限元的弹性裂缝问题模拟方法。 为解决上述技术问题，本发明的技术方案如下： 基于稳定广义有限元的弹性裂缝问题模拟方法，包括以下步骤： S1：根据裂缝问题GFEM/XFEM构建具有集合富集策略的GFEM/XFEM； S2：采用线性Heaviside函数对富集策略中的富集函数进行修正； S3：改变标准FEM的有限元PU函数，构造新型的SGFEM基本函数； S4：基于局部主成分分析技术对SGFEM基本函数进行处理，消除单个节点多个富集 函数导致的冗余，得到SGFEM模型； S5：通过SGFEM模型对裂缝问题进行求解，完成裂缝问题的模拟。 其中，所述步骤S1过程具体为： 区域Ω被剖分为拟正则三角形或四边形网格单元es,网格的尺寸参数用h表示，网 格是简单的、固定的，且与裂缝ΓO无关，{(xi，yi)：i∈Ih}记为网格节点集；令φi，i∈Ih为标 准的有限元函数，而 是与φi的支撑集；GFEM/XFEM的主要思想是通过使用PU 函数[7,6,10,13]将有限元函数和表达真解性质的特殊函数耦合起来，达到高精度的逼近 效果，这些特殊函数称为富集函数；裂缝问题GFEM/XFEM的近似函数uh如下： 7 CN 111597649 A 说　明　书 3/17 页 其中IH为与裂缝相交的单元的节点集，但是要除去支撑集包含裂尖的节点，ai、bi、 表示中间变量，Sj表示中间函数；Is为与裂尖为中心、半径为R的圆B(O，R)内部的节点集， 这种GFEM/XFEM被称为具有几何富集策略的GFEM/XFEM；在式(2)中，函数 为Heaviside函数，用于模拟真解在裂缝处的不连续性，而 称为裂尖加强函数，其中，R是富集范围的半径，r,θ是极坐标，数学表达式的中间 变量；利用富集函数H和 完成GFEM/XFEM的构建。 上述方案中，由于富集函数H和 的引入，导致它们与有限元函数之间发生线性相 关性，使得刚度矩阵的条件数比有限元大很多，从而在求解线性方程组时可能导致显著的 截断误差，甚至可能导致数值模拟过程的失败。因此，采用稳定广义有限元法的思想改进传 统GFEM/XFEM的条件数，并且提高逼近误差，改进的手段有修正富集函数、改变PU函数，局部 主成分分析几个方面。 其中，所述步骤S2过程具体为： 在式(2)中，采用线性Heaviside函数 代替传 统GFEM/XFEM的Heaviside函数H，然后 和 修正如下： 其中 是有限元插值算子，即对于一个连续函数F， 其中，参数v、φj均为数学表达式的中间变量；至此，得到基于修正后的富集函数， 构建具有集合富集策略的GFEM/XFEM。 上述方案中，由式(3)可以发现，富集函数减掉了它们的有限元插值，这是减轻其 与有限元函数线性相关性的举措之一[1,9,16,17,18]。 其中，所述步骤S3具体为：将式(2)中，标准的FEM函数φi作为PU函数，这也是刚度 矩阵条件数变坏的原因之一，参见[11,17]的论述。因此，将PU函数修改为高阶多项式PU函 数，具体为，令： Q0＝(1-ξ)2(1 2ξ)，Q1＝ξ2(3-2ξ)，ξ∈[0，1] 为一个一维参考单元[0,1]上的PU函数，根据此函数得到二维参考单元[0，1]× [0，1]上的PU函数 具体如下： 8 CN 111597649 A 说　明　书 4/17 页 为了得到任一实际单元es上的PU函数，令(x，y)＝Fs(ξ，η)为参考单元到es上的仿 射变换，则es上的PU函数为 将这些单元PU函数根据节点组装起来便得到了所需的PU函数Qi，i∈Ih；基于修正 后的富集函数(3)和新的PU函数Qi，得到新型的SGFEM基本函数表达式： 式(4)即为新型的SGFEM基本函数表达式，根据[16,18]中的思想可以数学上证明 该SGFEM可以达到最优收敛阶。 其中，所述步骤S4具体为：在式(4)中发现，有些节点富集了多个函数，例如IH中的 每个节点富集三个函数，IS中的每个节点富集四个函数，而IH∩IH中的每个节点富集七个函 数。因此，用 表示每个富集节点(xi，yi)的富集函数，则有： 显然对应于i∈IH，i∈Is，i∈IH∩Is，α分别等于3，4，7，每个节点的多个富集函数 之间的线性相关性是刚度矩阵条件数很大的另一个来源，为此，提出一种局部主成分分析 [8](local  principal  component  analysis,LPCA)技术，以消除单个节点多个富集函数导 致的冗余；  因为弹性力学方程是向量值方程，对于任意i∈IH∪Is，表示Ei关于x-和y-方向 的基函数如下： 对任意i∈IH∪Is，记 为函数 在内积 下的协方差矩阵；显然的， 是总刚度矩阵A的一个α×α的子矩阵，基于协方 差阵进行子成分分析PCA，得到α×α矩阵 和 其中： 每列包含一个主要成分的系数， 由各主成分所占的百分比组成；根据PCA性 质，新的主成分函数为： 在内积(5)下是正交的，并且可以根据向量 确定各主成分的贡献，删 除 的主成分函数，λ为预设的参数，这里采用λ＝10-10，这是一个非常小的百 9 CN 111597649 A 说　明　书 5/17 页 分比；LPCA不会导致收敛性下降，富集函数知识重新组合了，原有的逼近空间并没有改变， 而且只有“贡献”极小的冗余被删除了，此外LPCA可以根据基于SGFEM基本函数(4)对应的刚 度矩阵执行，不需要大量的额外计算。从这个意义上，LPCA可以视为求解线性系统的一个预 处理算法。 将LPCA视为求解线性系统的一个预处理算法，其具体实现过程为： 基于富集函数 整合刚度矩阵A和载荷向量b，对于任意节点(xi，yi)，i∈IH∪Is排 列多重富集函数的下标为Ji，...，Ji α-1，并从A中提取子矩阵 为 对于每个(xi，yi)，i∈IH∪Is，基于 执行PCA获得 和 并更新刚度矩阵A 和载荷向量b为： 对于每个(xi，yi)，i∈IH∪Is，如果 更新刚度矩 阵A和载荷向量b为： A(Ji j-1，：)＝0，A(：，Ji j-1)＝0， A(Ji j-1，Ji j-1)＝1，b(Ji j-1，：)＝0 对富集函数 执行与上述相同的过程，对刚度矩阵A和载荷向量b进行更新，获得 LPCA之后的新的刚度矩阵A和载荷向量b，从而得到SGFEM模型。 其中，所述步骤S5中通过SGFEM模型对裂缝问题进行求解，即是对线性方程组进行 求解，具体为： 将线性方程组尺度化： 令Eii＝(Aii)-1/2得到一个对角矩阵E，刚度矩阵A和载荷向量b尺度化后得到EAE、 Eb； 求解尺度化后线性方程组： EAEu＝Eb    (6) 逆预处理： 对于尺度化后得到的解u进行逆尺度化得到u＝Eu；同时，还需对u根据LPCA预处理 过程进行逆预处理： 基于富集函数 整合解向量u，对于任意节点(xi，yi)，i∈IH∪Is，排列多重富集函 数的下标为Ji，...，Ji α-1，并从A中提取子矩阵 为： 对于每个(xi，yi)，i∈IH∪Is，基于 执行PCA获得 和 若 10 CN 111597649 A 说　明　书 6/17 页 更新 和解向量u为： 对于每个(xi，yi)，i∈IH∪Is，更新解向量u为： 对富集函数 执行与上述相同的过程，获得逆LPCA之后的新的解向量u；从而对裂 缝问题的求解，完成裂缝问题的模拟。 其中，基于稳定广义有限元的弹性裂缝问题模拟方法还包括对SGFEM模型进行并 行化处理，利用并行化后的SGFEM模型对裂缝问题进行求解，完成裂缝问题的模拟。 其中，所述的对SGFEM模型并行化处理的过程具体为：将SGFEM模型的根据已有的 标记筛选出需要进行LPCA的节点，将节点进行离散后得到N个单元，根据计算机进程个数p 对节点进行划分，其中N不必被进程p整除；前p-1个进程处理 个单元，p号进程处理 余下N-nel(p-1)个单元；在每个进程中独立组装刚度矩阵A和载荷向量b，最后聚集到某一 特定进程中；进行LPCA时，会在每个节点根据A得到 并更新矩阵A和向量b，从而完成 SGFEM模型的并行化处理。 上述方案中，SGFEM模型跟FEM相比有很大不同，因此其并行化算法需要新的设计。 将求解区域进行离散后得到N个单元，根据计算机进程个数p对区域进行划分(单元数N不必 被进程数p整除)：前p-1个进程处理 个单元，p号进程处理余下N-nel(p-1)个单元。 在每个进程中独立组装刚度矩阵A和载荷向量b，最后聚集到某一特定进程(如0号进程)中。 注意到，组装刚度矩阵和载荷向量时不同进程间不需要数据通信。由于每个子区域生成的 刚度矩阵采用稀疏存储方式，最后进行聚集操作时数据通信量很小，花费时间远小于数值 计算本身。 上述方案中，对于LPCA，由于只有在裂缝附近的节点需要进行分析。如果将全部节 点根据进程数目划分会，则部分进程计算量很小、部分进程计算量较大，导致并行效率低 下。我们首先根据已有的标记筛选出需要进行LPCA的节点，再根据进程数按上述方法对节 点进行划分。进行LPCA时，可以在每个节点根据A得到 并更新矩阵A和向量b。 其中，采用并行化的Krylov子空间方法求解并行化后的SGFEM模型，即并行求解线 性系统EAEx＝Eb得到x，在对解向量x逆尺度化后，采用类似LPCA的方法进行逆LPCA对裂缝 问题进行求解，完成裂缝问题的模拟。 与现有技术相比，本发明技术方案的有益效果是： 本发明提供的一种基于稳定广义有限元的弹性裂缝问题模拟方法，改进传统 GFEM/XFEM的精度和条件数，使得裂缝问题的数值模拟更加精确和稳健，由于裂缝问题是结 构分析技术的关键环节之一，因此本技术方案对工程力学中的结构分析领域有重要的促进 作用。另外，本方法设计高度自动化和标准化，既可以嵌入到当前结构分析商业软件中，促 11 CN 111597649 A 说　明　书 7/17 页 进这些软件的升级，又可以作为工程软件自主开发的技术汇集。最后，本发明的技术方案是 关键工程软件发展的步奏之一，算法创新性强，模拟精度高，软件架构清晰合理，可嵌入性、 扩展性强，并行化程度高，具有很大的发展潜力和应用前景。 附图说明 图1为现有技术的裂缝问题表示示意图；ΓD和ΓN分别是本质边界和自然边界。(x， y)和(r，θ)分别是原点为O的直角坐标系和极坐标系。 图2为本发明所述方法流程示意图； 图3为SGFEM求解弹性裂缝问题流程图； 图4为一实施例中带有裂缝的区域表示示意图；裂缝Γo以非0和π的角度与网格相 交。节点○被Heaviside函数富集；节点×被奇异函数富集； 图5为一实施例中XFEM/GFEM和SGFEM的H1误差示意图； 图6为一实施例中XFEM/GFEM和SGFEM的SCN示意图； 图7为在求解问题规模固定的情况下不同处理器数目所需的计算时间的示意图； 图8为当处理器数目固定时，求解不同规模问题所需时间示意图。