技术摘要：
本发明提供了一种基于子空间表示和全局消歧方法的偏标记学习方法。该方法包括：构建特征矩阵和候选标记矩阵；基于构建特征矩阵和候选标记矩阵，构建特征子空间学习模型和标记全局消歧模型；综合特征子空间学习模型和标记全局消歧模型得到混合模型，采用交替优化方法求  全部
背景技术：
偏标记学习可以被看作一种弱监督的学习框架，这种学习框架的目的是从有候选 标签集合的样本中学到一个多分类模型。这种学习框架在现实社会中有着广泛的应用，比 如：自动标注系统，来自不同背景的人做了不同的标注，但是其中只有一个标记是正确标 注；一篇新闻报道出现了多人的名字和一张合照，我们需要把人名与合照中的人脸匹配。现 有的偏标记学习方法可以被分作三类，平均消歧的学习策略、辨识消歧的学习策略和非消 歧的学习策略。 平均消歧策略认为每个标签对学习模型做了相同的贡献，并且通过平均化模型输 出对测试样本做出预测。针对这个策略的代表方法有：基于k近邻的平均消歧方法，基于最 小化损失函数的消歧方法和基于最小化重构损失的消歧方法等等。基于平均消歧策略的方 法比较直观，容易实现。但是因为在训练模型的过程中真实标记容易受到伪标记影响，训练 模型的效果受到影响。 辨识消歧策略把真实标记看作一个隐变量，通过迭代达到最大化模型输出。辨识 消歧策略算法主要基于两大准则：极大似然准则 和最大化间隔准则 基于辨识消歧策略的方法，比基于平 均消歧策略的方法性能的准确率更优，但是也存在着一个潜在的缺陷，训练得到的标记可 能是伪标记，而不是真实标记。 现有技术中的偏标记学习方法的缺点包括： 1)消歧策略对每个训练示例单独消歧，忽略了偏标记学习的全局标记语义信息， 消歧得到的真实标记有待进一步改进； 2)现有的偏标记学习策略倾向于直接利用原始特征空间学习，但是在高维数据 中，冗余特征不可避免地会混杂在原始数据中，这样不仅会增加训练过程的时间和空间开 销，并且会降低模型的泛化性能。
技术实现要素：
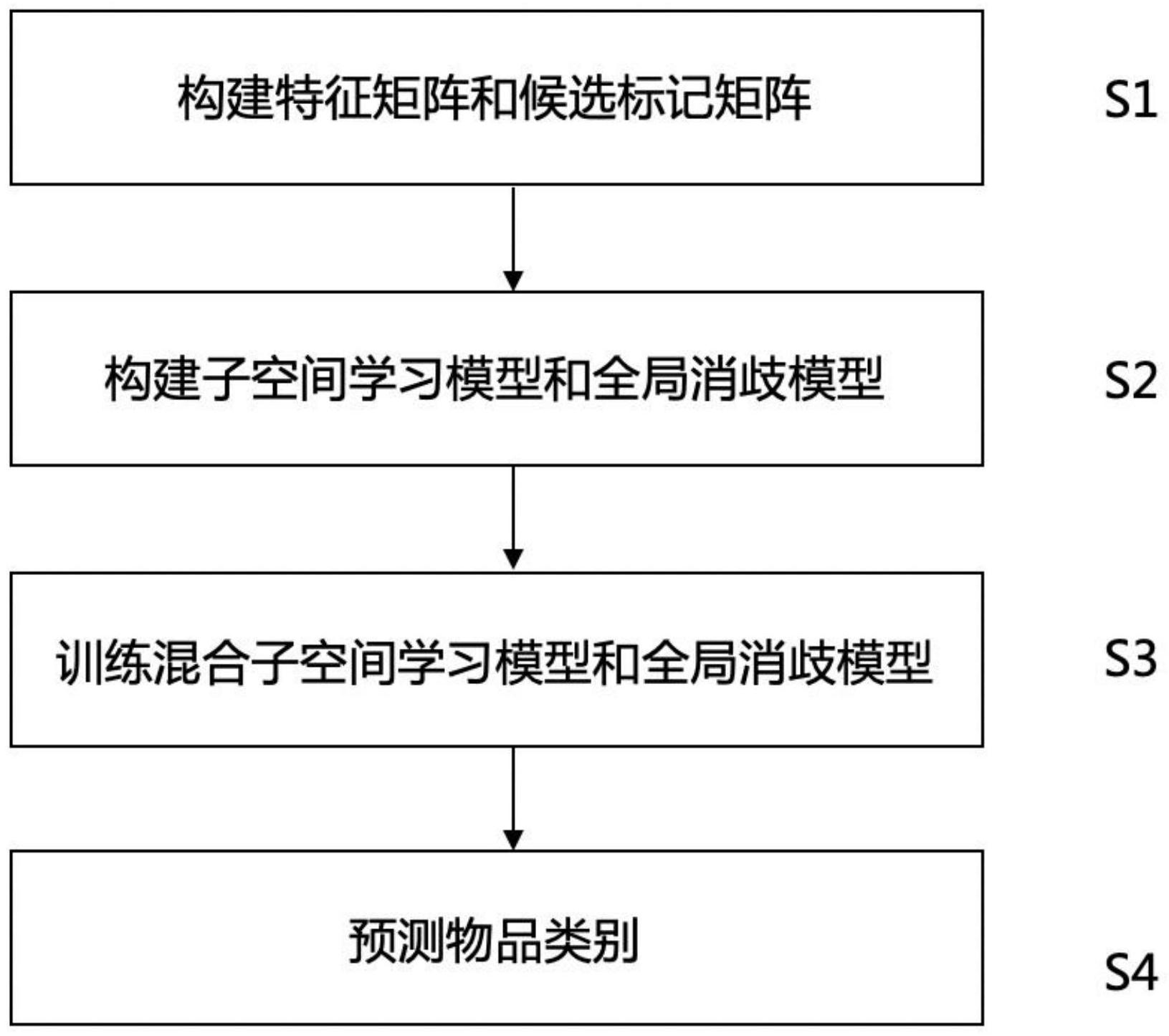
本发明的实施例提供了一种基于子空间表示和全局消歧方法的偏标记学习方法， 以克服现有技术的问题。 为了实现上述目的，本发明采取了如下技术方案。 一种基于子空间表示和全局消歧方法的偏标记学习方法，包括： 构建特征矩阵和候选标记矩阵； 基于所述构建特征矩阵和候选标记矩阵，构建特征子空间学习模型和标记全局消 5 CN 111581467 A 说　明　书 2/10 页 歧模型； 综合所述特征子空间学习模型和所述标记全局消歧模型得到混合模型，采用交替 优化方法求解所述混合模型，得到多分类模型、映射矩阵和偏标记置信度矩阵； 根据所述多分类模型和所述映射矩阵对未见示例进行分类，计算出所述未见示例 的多个标记值，将预测置信度最高的标记值对应的标记确定为所述未见示例所属的标记类 别。 优选地，所述的构建特征矩阵和候选标记矩阵，包括： 构建特征矩阵X∈[0，1]dxn，其中d和n分别表示特征维度数目和样本数目，构建候 选标记矩阵Y∈{0，1}mxn，其中m和n分别表示类别数目和样本数目，初始化标记置信度矩阵P ∈[0，1]mxn，其中m和n分别表示类别数目和样本数目，P的数值越接近于1，说明该标记是示 例的真实标记的可能性越大；P的数值越接近于0，说明该标记是示例的真实标记的可能性 越小。 优选地，所述的基于所述构建特征矩阵和候选标记矩阵，构建特征子空间学习模 型和标记全局消歧模型，包括： 构建特征子空间学习模型，利用特征子空间学习模型学习得到新的特征表示，生 成映射矩阵 其中d与分别表示原始特征空间的维度与子空间的特征维度； 构建标记全局消歧模型，利用标记全局消歧模型训练得到新的特征表示和候选标 记矩阵，利用所述标记全局消歧模型生成偏标记置信度矩阵P∈[0，1]mxn，多分类模型 其中其中d′与m分别表示子空间的特征维度与类别数目。 优选地，所述的构建特征子空间学习模型，利用特征子空间学习模型学习得到新 的特征表示，生成映射矩阵 其中d与d′分别表示原始特征空间的维度与子空间 的特征维度，包括： 构建子空间学习模型，生成映射矩阵 使用K近邻的方法构建示例的相似 度矩阵 构建图拉普拉斯矩阵 L＝D-S，D是一个对角矩阵，对角元素为相 似度矩阵S每一行的和，对所述映射矩阵 加上图拉普拉斯约束Tr(QTXLXTQ)； 设正交约束QTQ＝Id‘，其中Id′是尺寸为d′的单位矩阵，采用了最小二乘损失学习新 生成的特征表示与标记空间的映射关系，合并各项后，子空间学习模型的目标函数表示如 下： s.t.QTQ＝Id‘ 其中，λ1为超参数，用于调节正则项在损失函数中的比重，XT代表X的转置，PT代表P 的转置。 优选地，所述的构建标记全局消歧模型，利用标记全局消歧模型训练得到新的特 征表示和候选标记矩阵，利用所述标记全局消歧模型生成偏标记置信度矩阵P∈[0，1]mxn， 多分类模型 其中其中d‘与m分别表示子空间的特征维度与类别数目，包括： 构建全局消岐策略模型，生成映射矩阵和偏标记置信度矩阵P∈[0，1]mxn。 6 CN 111581467 A 说　明　书 3/10 页 在训练全局消歧策略模型的过程中，利用标记上下文语义信息从整体对偏标记候 选矩阵消歧，生成偏标记置信度矩阵P∈[0，1]mxn，对偏标记置信度矩阵P加上l1的范数约 束，对偏标记置信度矩阵P加上图拉普拉斯约束Tr(PLPT)，在偏标记置信度矩阵P中引入不 等式约束，确保偏标记置信度矩阵P中的每一项都大于等于零，并且小于等于原来的候选标 记； 合并各项后，全局消岐策略模型的目标函数表示如下： s.t.0≤P‘≤Y 其中，λ2，β为超参数，用于调节正则项在损失函数中的比重。 优选地，所述的综合所述特征子空间学习模型和所述标记全局消歧模型得到混合 模型，包括： 生成多分类模型 对多分类模型 增加Frobenius范数约束， 使用相同的正则化参数λ控制特征的语义一致性和标记的局部一致性，合并各项后，综合了 子空间学习模型和全局消歧模型的混合模型的目标函数表示如下： s.t.0≤P≤Y QTQ＝Id‘。 优选地，所述的采用交替优化方法求解所述混合模型，得到多分类模型、映射矩阵 和偏标记置信度矩阵，包括： S3-1：对所述混合模型初始化，初始化离散混合模型： P＝Y； Q＝eye(d，d′) S3-2：固定P，Q，更新W:基于交替优化算法，求解模型W等价于优化以下目标函数 对以上目标函数求导，并让求得的导数为0，W的具体的更新规则如下： W＝(QTXXT 2α)-1QTXPT S3-3：固定W，P，更新Q；固定W，Q，求解模型P，等价于优化以下目标函数问题 s.t.QTQ＝Id‘ 参数Q通过梯度下降的方法求出，对以上目标函数求导，具体Q的更新规则分为两 步： 第一步更新Q： Q＝Q-θ(XXTQWWT 2λXLXTQ-XPTWT) 使用Armijo准则来决定更新的步长θ； 第二步，对Q归一化，满足约束QTQ＝Id′； 7 CN 111581467 A 说　明　书 4/10 页 S3-4：固定Q，W，更新P：混合模型的目标函数等价于如下优化问题 s.t.0≤P≤Y 关于P的目标函数分为两部分， 和f(P)=β| |P||1，采用近端梯度下降的方法更新P，具体步骤如下： 求得近端梯度下降的Lipschitz连续性系数，借助Lipschitz连续性系数把关于P 的目标函数化为Frobenius范数和1范数的和； g′(P)＝P-WTQTX 2λPL ||g(P1)-g(P2)||F＝||(In 2λL)(P1-P2)||F ≤Lf||P1-P2||F σmax(·)代表了矩阵的最大特征值，Lipschitz连续性系数为 Lf＝σmax(In 2λ) 其次，将目标函数化为F范数和一范数的和的形式。 将目标函数带入求解： 其中， S3-7：重复执行S2-2到S3-4，不断交替更新参数W，Q，P，直到满足迭代停止条件，混 合模型收敛，输出混合模型的最优解(P*，Q*，W*)。 优选地，所述的迭代停止条件为目标函数值小于某个预设定阈值；或者P，Q和W的 每一位都不再发生变化；或者达到迭代的最大次数。 优选地，所述的根据所述多分类模型和所述映射矩阵对未见示例进行分类，计算 出所述未见示例的多个标记值，将预测置信度最高的标记值对应的标记确定为所述未见示 例所属的标记类别，包括： 根据映射矩阵Q和多分类模型W对未见示例x*进行分类，计算出未见示例x*的标记 值y＝arg  maxWTQTx*，WTQTx*是一个向量，每个向量的取值对应一种标记的预测置信度值，标 记的预测置信度值由WTQTx*得到，y的取值范围为大于0的实数，将预测置信度最高的标记值 对应的标记确定为未见示例x*所属的标记类别。 由上述本发明的实施例提供的技术方案可以看出，本发明实施例提出了一种基于 特征子空间表示和标记全局消歧方法的偏标记学习方法，该方法可同时利用特征子空间表 示法和标记全局消歧方法，同时从特征和标记两方面解决偏标记学习问题。与现有偏标记 学习算法相比，本发明方法在解决偏标记学习问题的问题上有更优秀的表现。 本发明附加的方面和优点将在下面的描述中部分给出，这些将从下面的描述中变 8 CN 111581467 A 说　明　书 5/10 页 得明显，或通过本发明的实践了解到。 附图说明 为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用 的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本 领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的 附图。 图1为本发明实施例提供的一种基于子空间表示和全局消歧方法的偏标记学习方 法的处理流程图； 图2为本发明实施例提供的一种混合模型的训练过程流程图； 图3为本发明方法与现有偏标记学习方法的对比实验结果。