技术摘要：
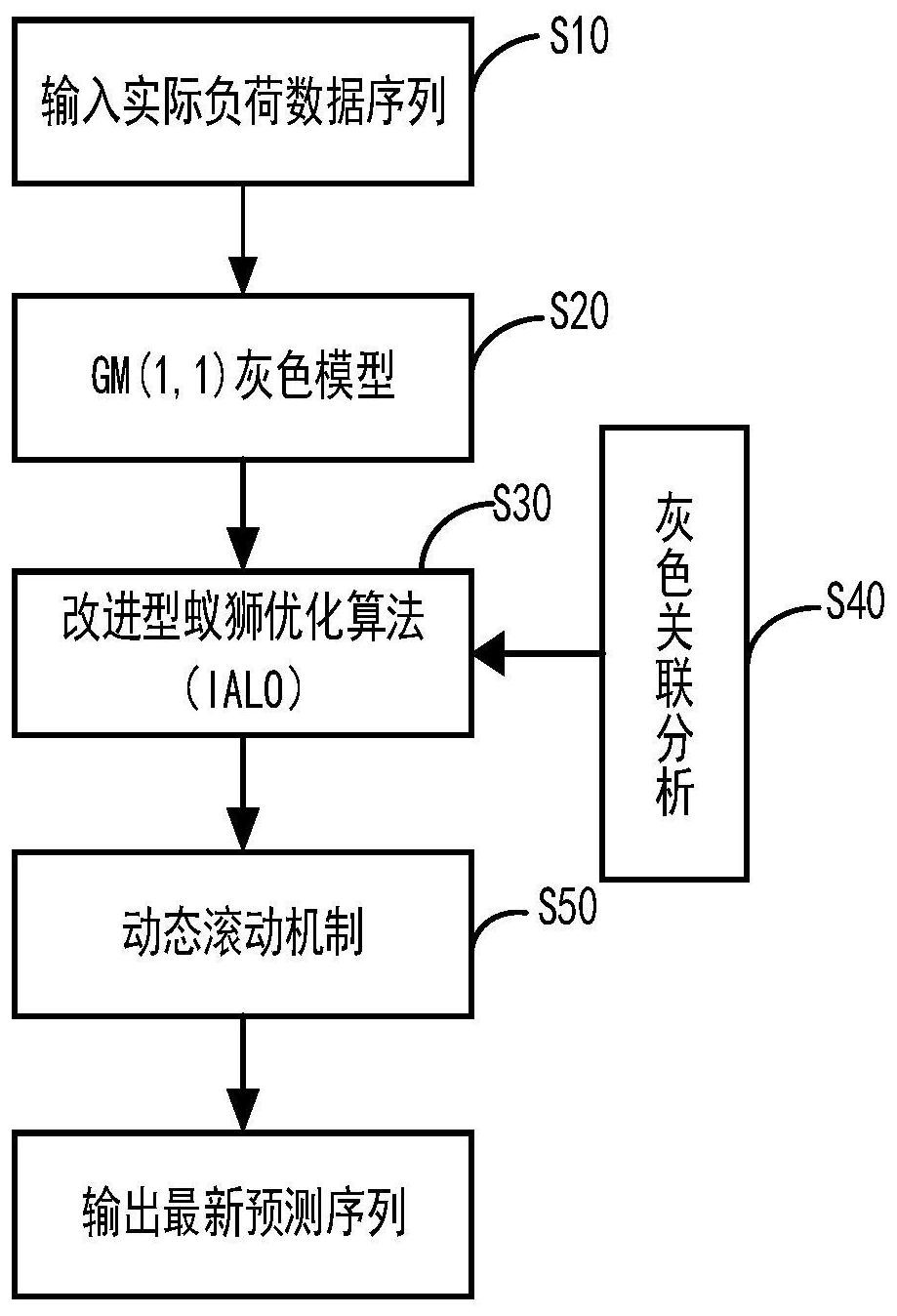
一种电力负荷中长期预测模型的性能提升方法，所述方法包括以下步骤：S10：输入实际负荷数据序列X(0)，并进行一次累加生成累加负荷数据序列X(1)；S20：建立GM(1,1)灰色系统模型；S30：建立IALO优化GM(1,1)模型；S40：基于灰色关联分析重新构建IALO中的适应度函数，二次  全部
背景技术：
准确的中长期负荷预测是制定合理的电力系统发展规划的前提，也是实现电网安 全经济运行的重要保障。我国中长期电力负荷的发展既有逐年增长的确定性，又有随机波 动的不确定性，可视为一种典型的灰色系统，因此邓聚龙教授提出的灰色模型GM(1,1)及其 优化模型在中长期负荷预测中得到了较为广泛的应用。 但中长期电力负荷由于受到经济、气候等因素的影响，常呈现一定的突变性，直接 利用原始负荷数据建立GM(1,1)模型，可能会导致模型误差较大或拟合效果较好而预测效 果较差。随着基础理论研究的逐步深入，人们开始利用群体智能算法来不断优化灰色模型 参数以提高模型的预测精度，其中蚁狮优化算法(ALO，以下简称为ALO)是最近提出的一种 自然元启发式算法。ALO算法的原理是模仿了自然界中的蚁狮狩猎机制，相比于其它优化算 法具有收敛速度较快、求解效率较高等特点，但是ALO算法在某些复杂的优化问题上具有不 平衡的勘探开发能力的缺点，从而在实际求解过程中常会陷入局部最优的问题。此外，ALO 算法利用平均相对预测误差最小为目标构建适应度函数来筛选最优模型参数值，常常会导 致模型预测精度高而拟合精度低的问题，预测结果的片面性和局限性也将会使灰色模型预 测的可信度进一步降低。
技术实现要素：
为了克服上述现有技术的不足，本发明提供了一种电力负荷中长期预测模型的性 能提升方法，可以有效地解决ALO-GM(1,1)模型自身的局限性问题和显著地提升预测精度。 为解决上述技术问题，本发明具体采用以下技术方案。 一种电力负荷中长期预测模型的性能提升方法，其特征在于，所述方法包括以下 步骤： 步骤S10：输入实际负荷数据序列X(0)，并进行一次累加生成累加负荷数据序列X (1)； 步骤S20：建立GM(1,1)灰色系统模型； 步骤S30：建立改进型蚁狮算法(IALO)优化GM(1,1)模型； 步骤S40：基于灰色关联分析重新构建改进型蚁狮算法(IALO)中的适应度函数，二 次优化GM(1，1)模型参数a和b，其中a为模型的发展系数，b为模型的协调系数； 步骤S50：通过多轮改进型蚁狮算法(IALO)动态滚动过程不断修正GM(1，1)模型参 数a、b值以获得最新负荷数据序列，最终根据不断更新的负荷数据序列得到全部目标预测 点。 本发明还进一步采用以下优选技术方案： 5 CN 111582535 A 说　明　书 2/8 页 在所述步骤S10中， 输入电力负荷的实际值序列为X(0)＝{x(0)(1)，x(0)(2)，...，x(0)(p)}， 经过一次累加生成累加负荷数据序列为X(1)＝{x(1)(1)，x(1)(2)，...，x(1)(p)}，其 中x(0)(p)是时间p点的负荷实际值； 所述步骤S20包括以下步骤： S201：在所述步骤S10输入的实际负荷数据序列和累加负荷数据序列的基础上，建 立灰色系统模型方程： S202：根据累加负荷数据序列X(1)满足指数增长的规律，建立一阶白化线性方程： S203：设参数向量 其中 S204：根据参数向量 求解S202中的方程获得时间响应函数： 对所述时间响应函数进行累减还原处理，得到预测序列 在所述S201中建立的灰色系统模型方程为 x(0)(k) az(1)(k)＝b 其中，a为模型的发展系数，b为模型的协调系数。 所述步骤S30包括以下步骤： S301：设置改进型蚁狮算法IALO的五个参数，所述参数包括蚂蚁和蚁狮的数量 Agents_no、变量数目dim、最大迭代次数Max_iteration、变量下限lr＝[lr1，lr2，...]以及 变量上限ur＝[ur1，ur2，...]； S302：位置初始化，即随机生成蚂蚁和蚁狮的位置，得到两者的位置矩阵： S303：选择初始精英，计算蚁狮的适应度值： S304：使用矩阵MOAL存储蚁狮的适应度值： 6 CN 111582535 A 说　明　书 3/8 页 S305：在矩阵MOAL中选择蚁狮适应度值中的最大值作为精英适应度值，其中精英是 指在每一次迭代中根据适应度值最大值而得到的最佳蚁狮。根据蚁狮适应度函数，将每次 迭代中求得的最大适应度值对应的蚁狮作为初始精英，每只蚁狮(包括精英)仅对应一个适 应度值。 在所述步骤S302中， 其中Mant、Mantlion矩阵的条目通过以下公式计算： A*j或AL*j＝rand*(urj-lrj) lrj 式中：A*j和AL*j代表矩阵的第j列的值；rand是在间隔[0，1]中均匀分布生成的随 机数；urj和lrj分别表示第j个变量的上限和下限；n表示位置矩阵的第n行，n＞1；d表示位置 矩阵的第d列，d＞1。 在所述步骤S303中， 其中，f[(a，b)i]为蚁狮适应度函数；i为蚁狮的数量，i≥1；x(0)(k)为时间k点的负 荷实际值； 为时间k点的负荷预测值；ρ为分辨系数，0＜ρ＜1，一般取ρ＝0.5。 所述步骤S40包括以下步骤： S401：开始迭代，获取第i只蚂蚁的位置： S402：根据适应度值大小比较选择最终精英，当满足 的条 件时，更新蚁狮的位置和适应度值，然后重新确定精英，如果存在任何蚁狮的适应度值比前 一次迭代确定的精英更高，则更新其位置，得到最终精英，其位置为模型参数a和b的最优 值，即模型参数向量 等于精英的位置矩阵。 在所述步骤S401中，通过以下公式获取第i只蚂蚁的位置， 其中， 是第t次迭代中第i只蚂蚁的位置； 是在第t次迭代中由轮盘赌算法 选择的狮子周围的随机游走；elite是精英的位置； 是第t次迭代中围绕精英的随机游 走；其中，c1、c2是加速系数，为非负常数。 所述步骤S50包括以下步骤： S501：根据实际负荷序列X(0)＝{x(0)(1)，x(0)(2)，...，x(0)(p)}构建IALO-GM(1，1) 模型， 然后得到预测序列 其中q为未 7 CN 111582535 A 说　明　书 4/8 页 来时间点，且q≥1。 S502：将实际负荷序列中x(0)(1)，x(0)(2)，...，x(0)(p)前p个数据点移除，然后在此 基础上加入原先得到的预测序列 重构 新的实际负荷序列。 S503：重复步骤S502，直到获得所有需要预测的目标负荷数据点。 与现有技术相比，本发明具有以下有益效果： 本发明基于现有灰色系统模型GM(1，1)和蚁狮优化算法(ALO)的基础之上，提供了 一种新的基于灰色关联分析的混合优化改进型灰色系统模型。该模型首先通过最新数据来 预测将来的数据点，根据最新数据通常反映研究对象的最新发展趋势和特征的动态特性， 提出了一种动态滚动机制，其次提出了基于灰色关联分析的改进型蚁狮优化算法(IALO)， 避免算法陷入局部最优以及确保预测结果最大程度地保持了原始负荷数据的内在变化规 律，最后将以上两方面的改进应用到基础GM(1，1)预测模型上，设计了一种基于灰色关联分 析的混合优化改进型灰色预测模型，从而可以显著提升GM(1，1)模型的预测精度，同时在中 长期电力负荷预测方面，该方法相比一些常用的群体智能算法具备更高的准确度，有效保 障了电力负荷预测模型的预测性能。 附图说明 图1为本发明的方法流程图； 图2为动态滚动机制的示意图。