技术摘要：
本发明涉及全控型电压驱动式功率半导体器件领域；公开了一种随机载荷下压接式IGBT器件性能稳健性优化设计方法，该方法包括以下处理步骤：基于待优化的压接式IGBT器件，选取设计目标和约束；提取应力分析相关结构并给定分析参数；建立热力耦合有限元模型；建立IGBT器件  全部
背景技术：
绝缘栅双极型晶体管(Insulated  Gate  Bipolar  Transistor，IGBT)是当前最为 典型一类全控型电压驱动式功率半导体器件。IGBT是能源变换与传输的核心器件，俗称电 力电子装置的“CPU”，广泛应用在轨道交通、智能电网、航空航天、电动汽车与新能源装备等 国家战略性新兴产业。压接式IGBT器件相比于传统焊接式IGBT模块具有双面散热、易于串 联、功率密度大和失效短路工作模式等优点，非常适用于电力系统等高压大功率应用场景。 典型的压接式IGBT从结构上大体一致：IGBT与FRD芯片先分别封装成子模组，各模组按照银 片、下钼片、芯片及上钼片依次堆叠在塑料框架中，同时IGBT子模组还设计有弹簧引针以连 接芯片栅极与电路板；将各子模组装入陶瓷管壳形成IGBT器件。这种压接方式采用弹性模 量较小的银片以均衡各子模组的压力，具有更简单、更紧凑的结构。 通过在IGBT器件上下表面施加压力，IGBT器件内部元件之间彼此贴合，从而实现 电气连接并构建散热通路。IGBT器件中子模组中各元件热膨胀系数不匹配，结构位置和热 功耗也存在差异，造成各子模组中元件之间接触压力存在差异，从而直接影响接触阻抗和 接触热阻。接触阻抗和接触热阻的不均衡，一方面会直接导致IGBT器件电气性能的大幅波 动，另一方面也会加剧温度和机械应力的不均衡，反过来又进一步恶化阻抗与热阻的平衡 度。由此可见，接触应力不均匀是电磁-温度-位移等多场耦合的核心问题，现已成为该领域 研究的重点和难点。值得指出的是，热不平衡问题的核心在于发热源，即IGBT中的芯片热 耗。由于IGBT器件工况复杂且恶劣，各子模组的芯片功耗不确定的，并具有时变特性，因而 呈现随机载荷的特征。 已有研究者对压接式IGBT器件的多场耦合机理进行了初步探索，并利用数值模拟 技术(如有限元分析)对其构建了多场耦合仿真模型。便阅文献后可知，构建实用的性能优 化模型的研究很少，在优化模型中考虑芯片热耗为随机载荷则未曾见诸于报道。究其原因 主要包括如下两个方面：首先，尽管多场耦合仿真模型的构建为结构优化奠定了一定基础， 然而选取合适的设计变量，结合工程实际建立设计目标和约束，从而构建有效的参数化结 构优化模型仍然是亟需解决的技术问题。其次，在设计目标和约束中如何考虑随机载荷，并 建立相应的性能稳健性度量函数，在本领域研究中仍然存在空白。再次，即便上构建了IGBT 性能稳健性优化模型，由于涉及耗时的多场耦合仿真模型并包含复杂的随机过程分析，给 出高效的并深具工程实用性的求解流程将极富挑战。 为此，针对压接式IGBT器件性能稳健性优化问题，构建有效的优化模型，并提出相 应的高效求解算法，对于提升IGBT器件设计水平并开发具有良好性能稳健性的新型压接式 IGBT产品，具有非常重要的工程意义。 如中国专利公开号CN  110765601  A，公开日为2020年2月7日，公开了一种基于 6 CN 111581901 A 说　明　书 2/14 页 IGBT热电耦合模型的IGBT结温估计方法，具体步骤包括,建立基于热敏参数法与双脉冲测 试原理的实验平台、交叉热耦合模型、功率损耗模型；利用热敏参数法建立二维耦合热阻网 络模型提取瞬态热阻抗参数，搭建交叉热耦合模型；基于双脉冲测试原理测试IGBT开关特 性，获取功率损耗模型参数，搭建功率损耗模型；基于交叉热耦合模型与功率损耗模型耦合 IGBT热电耦合模型，并估算IGBT结温。其并未考虑随机载荷的影响，不易解决IGBT中的芯片 中接触压力不均匀问题。
技术实现要素：
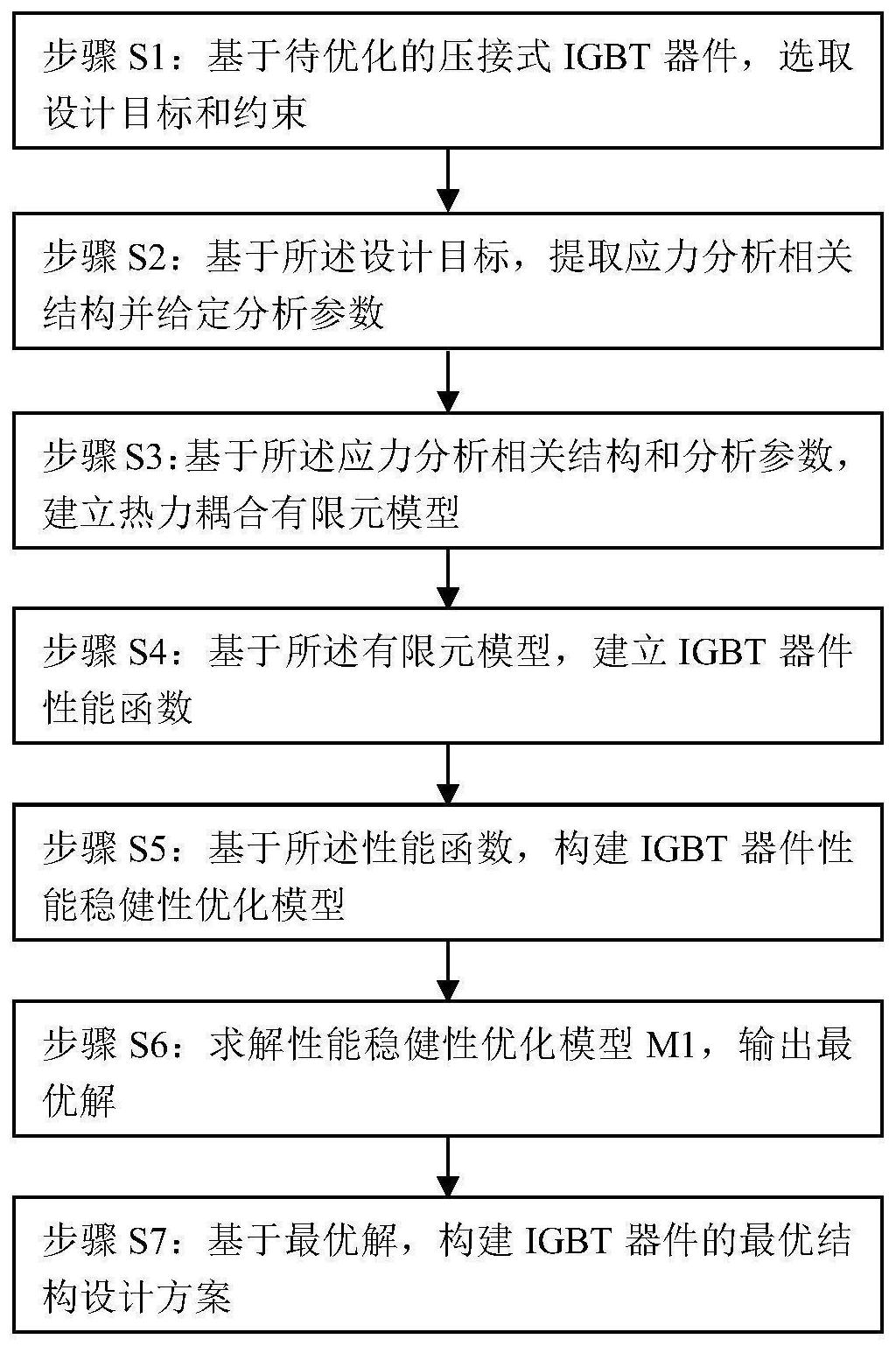
本发明要解决的技术问题是提供一种能解决IGBT中的芯片中接触压力不均匀问 题的随机载荷下压接式IGBT器件性能稳健性优化设计方法。 为了解决上述技术问题，本发明克服了现有技术的不足，采用了一种随机载荷下 压接式IGBT器件性能稳健性优化设计方法。首先，通过对IGBT器件进行热力耦合有限元分 析，建立基于芯片应力响应的性能函数；其次，选取芯片的最大应力和最小典型应力作为设 计目标和约束，建立了考虑芯片热载荷随机过程的IGBT性能稳健性优化模型；再次，提出相 应的求解流程，计算得到最优解，并给出了最优解到IGBT设计方案的转换方法。 具体包括以下步骤： S1：基于待优化的压接式IGBT器件，选取设计目标和约束； S2：基于所述设计目标，提取应力分析相关结构并给定分析参数； S3：基于所述应力分析相关结构和分析参数，建立热力耦合有限元模型； S4：基于有限元模型，建立IGBT器件性能函数S； S5：基于所述性能函数，构建IGBT器件性能稳健性优化模型M1； S6：求解性能稳健性优化模型M1，输出最优解； S7：基于最优解E*，构建IGBT器件的最优结构设计方案。 作为本发明进一步的改进，在步骤S1中，所述待优化的压接式IGBT器件包括FRD芯 片和IGBT芯片，所述设计目标选取为所述FRD芯片和IGBT芯片上的最大应力SU，用于获得所 述FRD芯片和所述IGBT芯片的各芯片最优应力均衡，所述约束选取为所述FRD芯片和所述 IGBT芯片的各芯片上的最小典型应力值ST应大于或等于额定应力S0，即ST≥S0，用于保证接 触截面的热传导。 IGBT器件包含n个第一子模组、第一集电极铜块、第一发射极铜块，所述第一子模 组分为两类：IGBT子模组和FRD子模型。所述每个n个子模组具有共同的结构组成，包括如下 元件：上钼片、芯片、银片、下钼片。所述IGBT子模型中的所述芯片被称为IGBT芯片，所述FRD 子模型中的所述芯片被称为FRD芯片。由于ST≥S0，保证了接触截面的热传导，从而得以实现 芯片散热，S0根据工程经验给定，所述各芯片中某一芯片的典型应力值为所述某一芯片中 间位置的应力。 作为本发明进一步的改进，所述典型应力值ST为所述FRD芯片或所述IGBT芯片的 中间位置的应力，所述额定应力S0根据工程经验给定。 作为本发明进一步的改进，在步骤S2中，所述应力分析相关结构包括第一集电极 铜块、第一发射极铜块和第一子模组中的相关结构，所述给定分析参数是指材料参数、相互 作用参数和载荷参数，所述材料参数是指所述各相关结构的材料机械特性与热特性参数， 7 CN 111581901 A 说　明　书 3/14 页 所述相互作用参数是指在第一上表面、第二下表面上与所述冷板之间的热交换系数CT、冷 板温度TS，所述载荷是指第一上、下表面承受的压力F、FRD芯片的热耗随机载荷P1、IGBT芯片 的热耗随机载荷P2，所述随机载荷P1、P2在其随机过程的任一时刻对应一随机变量，其均值 分别为uP1、uP2，标准差为vP1、vP2；随机载荷P1、P2在过程[t1 ,T]的自相关函数为CR1(τ|τ∈ [t1,T])、CR2(τ|τ∈[t1,T])，其中，t1、T表示所述过程的起始时刻和终止时刻，τ表示所述过 程中某一时间间隔。 此外，在上述改进中，所述材料参数具体包含：弹性模量、泊松比、热膨胀系数、热 传导率、比热容，所述材料参数可通过现有试验方法或查阅现有的材料手册得到； 所述相互作用参数CT和TS的值根据IGBT面临的实际工况给定； 所述随机载荷P1、P2的特征已知。 作为本发明进一步的改进，在步骤S3中，对所述IGBT器件应力分析相关结构建立 基于X方向和Y方向对称的1/4型有限元模型，在所述有限元模型中的边界条件设为：对下表 面建立固支边界条件，对第一区域和第二区域建立基于X方向的对称边界条件，对第三区域 和第四区域建立基于Y方向的对称边界条件；在所述有限元模型中的相互作用设为：在第二 上表面和第二下表面上建立表面热交换条件，其参数为CT、TS；在所述有限元模型中的载荷 设为：在第二上表面上施加均布压力F；对FRD芯片模型施加P1＝uP1的热载荷；对IGBT芯片模 型施加每芯片P2＝uP2的热载荷；选取耦合温度-位移稳态求解器对所述有限元模型求解，得 到待优化IGBT器件的应力响应，最后提取最大应力SU和最小典型应力ST。 此外，在上述改进中，在结构方面，所述有限元模型包括集电极铜块、发射极铜块 以及m个子模组，每一所述子模组包含：所述上钼片、所述芯片、所述银片、所述下钼片。 作为本发明进一步的改进，在步骤S4中，建立性能函数S的流程为： 步骤S4.1：定义所述有限元模型中的银片等效弹性模量向量E，E＝[E1 ,E2 ,..., Em]； 步骤S4.2：定义随机载荷向量P，其由随机载荷P1、P2构成，即P＝[P1,P2]； 步骤S4.3：将所述向量E中元素Ei,i＝1,2,...,m作为所述银片的弹性模量，将所 述向量P中元素P1、P2作为每一所述FRD芯片、IGBT芯片的热耗，输入到所述有限元模型中求 解得到相应的最大应力值SU和典型应力值ST，将SU和ST视作所述IGBT器件的两个性能函数， 其涉及的变量包含所述向量E、P，即：SU(E,P)和ST(E,P)。 作为本发明进一步的改进，在步骤S5中，建立优化模型M1的流程为： 步骤S5.1：选取向量E为设计向量，即向量E中元素Ei ,i＝1,2 ,...,m作为设计变 量； 步骤S5.2：设定Ei的取值范围ELi≤Ei≤ERi,i＝1,2,...,m，其中，ELi和ERi表示Ei 取值的上界和下界，ELi和ERi根据工程经验给定。ELi的取值范围优选为[0.1E0,0.4E0]，ERi 的取值范围优选为[0.5E0,E0]。 步骤S5.3：将过程[t1,T]离散成p个时刻，计为时间向量t＝[t1,t2,...,tp]，tp即所 述过程的终止时刻T；p的取值范围通常为[5,50]。在实际工程中，根据对随机过程的离散数 的选取根据所需计算精度选取。对于连续过程的离散处理，当离散数越多时则后续求解精 度越高，同时会为求解过程引入更大的计算量。 步骤S5.4：基于随机载荷Pi,i＝1,2的参数uPi,vPi,和自相关函数CRi，对时间向量t 8 CN 111581901 A 说　明　书 4/14 页 进行ns次的随机采样，每一过程样本均包含p个时刻的样本点；即对于Pi的第j个过程样本， 可写成向量Pi,j＝[Pi,j(t1) ,Pi,j(t2) ,...,Pi,j(tp)]，其中，i＝1,2；j＝1,2,...,ns；随机采 样次数ns的取值范围通常为[200,2000]。在实际工程中，随机采样的次数越多，计算精度越 高，同时也会引入更大的计算成本。 步骤S5.5：对于所述设计向量E，将Pi,i＝1,2的过程样本代入到性能函数SU(E,P) 和ST(E ,P)中，可得到ns个S的过程样本；对于SU、ST的第j个样本可分别写成向量S Uj ＝[S Uj (t1) ,S Uj (t2) ,...,S U(t )]、S T T Tj p j ＝[Sj (t1) ,Sj (t2) ,...,S Tj (tp)]； 步骤S5.6：对SU、ST的所有过程样本取极值，即S Umax＝max(S Uj j ) ,S Tmin Tj ＝min(Sj ) ,j ＝1,2,...,n ；max( )和min( )分别表示对向量元素选取最大值和最小值；S Umaxs j 组成ns维向 量SUmax＝[S Umax,S Umax,...,S Umax]，S Tmin组成n 维向量STmin＝[S Tmin Tmin Tmin1 2 ns j s 1 ,S2 ,...,Sns ]； 步骤S5.7：基于向量SUmax和STmin，构造IGBT性能稳健性优化模型M1： 其中，Rf(SU(E,P))为稳健性目标函数，Rg(ST(E,P))为稳健性约束函数，Rf和Rg均 内嵌了性能函数S而成为向量(E,P)的嵌套函数，Rf和Rg的表达式分别为：Rf(SU(E ,P))＝ mean(SUmax)，Rg(ST(E,P))＝mean(STmin)≥S0；其中mean表示向量均值计算。 理论上可以通过序列二次规划、拟牛顿算法等现有方法对步骤S5构建的模型M1进 行求解。然而，Rf(SU(E,P))和Rg(ST(E,P))各自嵌套了性能函数SU(E,P)和ST(E,P)，每次计 算SU和ST的值均需求解一次所述有限元模型。采用随机过程离散和随机采样以获得Rf和Rg， 每一次Rf和Rg需要计算ns*nt次SU(E,P)和ST(E,P)。再者，求解稳健性优化模型M1可能需要 多次(写成no)计算Rf和Rg。如此，整个计算过程需要调用所述有限元模型ns*nt*no次，在实 际工程中每次计算有限元模型均较为耗时(数分钟甚至数小时)，这将造成极其低下的计算 效率。为此，接下来给出一种高效求解M1的流程。 作为本发明进一步的改进，在步骤S6中，求解优化模型M1的流程为： 步骤S6.1：基于性能稳健性优化模型M1，构造确定性优化模型M2： 其中，uP表示由所述随机载荷P1，P2均值组成的向量，写成uP＝[uP1,uP2]； 步骤S6.2：设迭代步k＝1和初始点 采用现有的序列二次规划 算法对模型M2求解，输出当前迭代步的解E(k)＝[E (k) ,E (k) ,...,E (k)],SU(1) U (k)1 2 m ＝S (E ,uP)， ST(k)＝ST(E(k) ,uP)；对于确定性优化模型M2，由于并不涉及所述稳健性目标函数和约束的求 解，仅包含性能函数SU和ST，当m＝4时，仅需数十次调用所述有限元模型即可计算结束。 步骤S6.3：更新迭代步k＝k 1； 步骤S6.4：基于上一迭代步的解E(k-1)构造SU(E,P)的近似表达式LU(k)(E,P)和ST(E, 9 CN 111581901 A 说　明　书 5/14 页 P)的近似表达式LT(k)(E,P)： LU(k)(E,P)＝SU(E(k-1) ,u ) Σ (a (k)P i＝1:m i ·(E -E (k-1)i i )/Ei) Σi＝1:m(b (k)i ·(Ei-E (ki -1))2/E 2) Σ (c (k)·(P -u )/P ) Σ (d (k)i j＝1:2 j j Pj j j＝1:2 j ·(Pj-uPj)2/P 2j ) LT(k)(E,P)＝ST(E(k-1) ,u ) Σ (A (k)·(E -E (k-1)P i＝1:m i i i )/Ei) Σ (k)i＝1:m(Bi ·(Ei-E (ki -1))2/E 2) Σ (C (k)·(P -u )/P ) Σ (D (k)·(P -u )2/P 2i j＝1:2 j j Pj j j＝1:2 j j Pj j ) 其中，Σi＝1:m( )表示括弧中i取值1～m的求和计算；ai,bi,cj,dj,(i＝1,2,...,m；j ＝1,2)表示所述表达式LU(k)(E,P)的待定系数，Ai,Bi,Cj,Dj,(i＝1,2,...,m；j＝1,2)表示所 述表达式LT(k)(E,P)的待定系数,得到所述待定系数的表达式： 其中，以 为例，该运算表示性能函数SU在设计解(E(k-1) ,uP)处对变 量Ei求一阶偏导， 表示求二阶偏导，其他位置的 含义同理。 在第k次迭代步，求得近似表达式L(k)(E,P)中的待定系数的数值； 步骤S6.5：采用近似表达式LU(k)(E ,P)、LT(k)(E ,P)分别替代模型M2中性能函数SU (E,P)、ST(E,P)，计算当前迭代步的稳健性目标函数值和稳健性约束函数值：Rf(k)＝Rf(LU(k) (E,P))、Rg(k)＝Rg(LT(k)(E,P))，并进一步分别求取目标函数与约束函数值差：ΔSU(k)＝Rf (k)-S(E(k-1) ,u )、ΔST(k)＝S(E(k-1)P ,uP)-Rf(k)； 步骤S6.6：基于目标函数与约束函数值差，建立当前迭代步的稳健性优化模型M3： 采用现有的序列二次规划算法对模型M3求解，得到当前迭代步的解E(k)＝[E (k)1 ,E2 (k) ,...,E (k)m ]。模型M3与模型M2类型，由于并不涉及所述稳健性目标函数和约束的求解，仅 包含性能函数SU和ST，当m＝4时，仅需数十次调用所述有限元模型即可计算结束。 步骤S6.7：判断是否收敛，如收敛则输出最优解E*＝E(k)；否则，转入步骤S5.3；收 敛标准M4如下： 其中，norm( )表示向量求模计算，abs( )表示绝对值计算；e1和e2表示给定的收敛 限，e1、e2通常的取值区间为[0.1,0.001]；取值越小，计算精度越高，迭代步也越多。求解过 程经历了k次迭代后收敛到最优解E*，及相应的最大应力值SU*＝S(E*,uP)，最小典型应力值 10 CN 111581901 A 说　明　书 6/14 页 ST*＝S(E*,u )，稳健性目标函数值和约束函数值Rf*P 、Rg*。 作为本发明进一步的改进，在步骤S7中，构建所述IGBT器件的最优结构设计方案 的流程为： S7.1建立与所述银片的结构外形尺寸一致的银片初始构型，在所述银片初始构型 上设计镂空区域、边框区域； S7.2根据实际加工工艺要求，设置边框区域的边框宽度w≥w0，w0为初始边框宽度， 通常情况下银片外形结构为正方形薄片，具有一定的厚度，L为所述正方形的边长。 S7.3根据所述IGBT器件中银片与所述有限元模型中银片之间的对应关系，建立第 j个银片与Ei之间的函数式：E *＝1-(L-2*w )2i j /(L-2*w 2j 2) 。 S7.4将最优解E*代入到所述函数式中，计算得到最优设计方案wj,j＝1,2,...,n。 与现有技术相比，本发明的优点在于： 首先，在所述IGBT性能稳健性优化模型M1中将芯片最大应力、最小典型应力分别 定义为设计目标和约束，从而优化模型可以兼顾应力平衡和最小应力，相较于常规技术仅 考虑其中一个因素更为有利于提升IGBT的性能。其次，所述模型M1考虑了随机载荷的影响， 相较于常规技术将随机载荷假设为确定性参数，所提方法更有利于保证计算结果的稳健 性。再次，求解优化模型M1的流程较一般的方法在效率上提升了有极大的提升。最后，优化 解被直接转化成IGBT的结构设计方案，从而使得所提方法具有很好的工程实用性。本发明 有利于解决IGBT器件设计中产生的芯片应力不平衡问题。 附图说明 图1是本发明方法的流程示意图。 图2是本发明具体应用实例中IGBT器件的结构示意图。 图3是本发明具体应用实例中IGBT器件热力耦合有限元模型。 图4是本发明具体应用实例中待优化IGBT器件的应力响应。 图5是本发明具体应用实例中随机载荷P1的6个随机过程样本。 图6是本发明具体应用实例中随机载荷P2的6个随机过程样本。 图7是本发明具体应用实例中与P1、P U2对应的芯片最大应力S 的6个随机过程样本。 图8是本发明具体应用实例中与P1、P2对应的芯片最小典型应力ST的6个随机过程 样本。 图9是本发明具体应用实例中求解IGBT器件性能稳健性优化模型的流程示意图。 图10是本发明具体应用实例中求解IGBT器件性能稳健性优化模型的迭代过程。 附图标记：20、压接式IGBT器件；201～204、FRD子模组；2011、第一上钼片；2012、 FRD芯片；2013、第一下钼片；2014、第一银片；2015、第一框架；205～216、IGBT子模组；2051、 第二上钼片；2052、IGBT芯片；2053、第二下钼片；2054、第二银片；2055、第二框架；2056、引 针；217、第一集电极铜块；218、第一发射极铜块；219、集电极法兰；220、发射极法兰；221、管 壳；222、电路板；223～226、第一绝缘垫；2170、第一上表面；2180、第一下表面；30、有限元模 型；317、第二集电极铜块；318、第二发射极铜块；3051、第三上钼片；3052、IGBT芯片模型； 3053、第三下钼片；3054、第三银片；3170、第二上表面；3180、第二下表面；3171、第一区域； 3181、第二区域；3172、第三区域；3182、第四区域。 11 CN 111581901 A 说　明　书 7/14 页