技术摘要：
本发明公开了一种基于神经网络解决电磁逆散射问题的两步无相位成像法。在电磁逆散射成像领域，全波数据反演算法需要用到全波数据，然而全波数据的实际测量相当困难；无相位反演算法仅需要使用无相位总场数据，无相位总场数据的实际测量要容易很多，但是无相位反演算法  全部
背景技术：
电磁波逆散射成像是无损无接触式获取物体电磁或物理特性的一种重要的方法。 电磁检测方法已经广泛地应用在定位，微波遥感，地球物理探测，无损检测，生物医学成像 等多种领域。总的来说，电磁逆散射问题是应用被测物体对入射波的散射，通过测量物体外 部的散射场或其远场模式，反演或重构物体的物理、几何特性，包括其位置，尺寸，数量，边 界和电磁参数分布等。 在过去的几十年中，由于研究人员的不断努力，电磁逆散射成像技术变得越来越 成熟，已经开发出了许多不同的反演方法来更有效和可靠地探测区域内的未知散射体。但 是，不适定性和非线性仍然是解决电磁逆散射问题过程中所面临的两大困难。为了提高反 演的效率，有研究人员忽略了感兴趣域(Domain  of  Interest，DoI)中的多重散射效应，提 出了基于伯恩近似(Born  approximation,BA)和Rytov近似的线性方法。线性算法的运算量 比较小，计算速度也比较快，但近似条件比较苛刻，一般只用于弱散射体。为了应对强散射 体，建模中应包括多重散射效应，并开发非线性方法，例如变形伯恩迭代法(Distorted  Born  Iteration  Method ,DBIM)，对比源反演法(contrast  source-type  inversion  method，CSI)，子空间优化算法(Subspace-based  Optimization  Method,SOM)，双重子空间 法(Two-fold  SOM,TSOM)以及某些全局优化方法。非线性算法通过优化算法，逐次迭代逼近 真实解，应用范围比较广泛，其计算量比较庞大。近年来，神经网络算法逐渐渗透到各个研 究领域。在本领域，卷积神经网络(Convolutional  Neural  Network,CNN)已成功地应用于 非线性逆散射问题的解决方案中，并且基于CNN的反演方法在图像质量和计算速度方面均 优于传统的非线性反演算法。 上述提到的方法都是利用具有幅度和相位信息的散射场数据(全波数据)来重建 散射体的几何参数和物理性质。但是散射场幅度和相位的准确测量也一直是一个难点。相 位测量通常会带来相当大的困难和无法忽略的硬件成本，甚至当频率高到一定程度时无法 直接测出相位信息。因此，用散射场数据来重建散射体的要求限制了该技术在许多实际场 景中的应用。相比较而言，无相位总场的获取则要容易很多，于是研究人员们又提出了一些 利用无相位总场数据的方法来重建散射体，例如牛顿法(Newtons  method)，无相位子空间 优化算法(Phaseless  Data  Subspace-based  Optimization  Method,PD-SOM)，无相位对比 源反演法(Phaseless  Data  Contrast  Source  Inversion,PD-CSI)和无相位正则化对比源 反演法(Phaseless  Data  Multiplicative  Regularized,PD-MRCSI)。但无相位算法也存在 着缺点，例如它的抗噪声能力更差，并且具有更高的非线性度。总的来说，全波数据反演算 法和无相位反演算法的各有各的优缺点，因此研究出一种既能节省硬件成本，又能有效处 理高非线性的方法具有非常大的意义。 5 CN 111609787 A 说　明　书 2/6 页
技术实现要素：
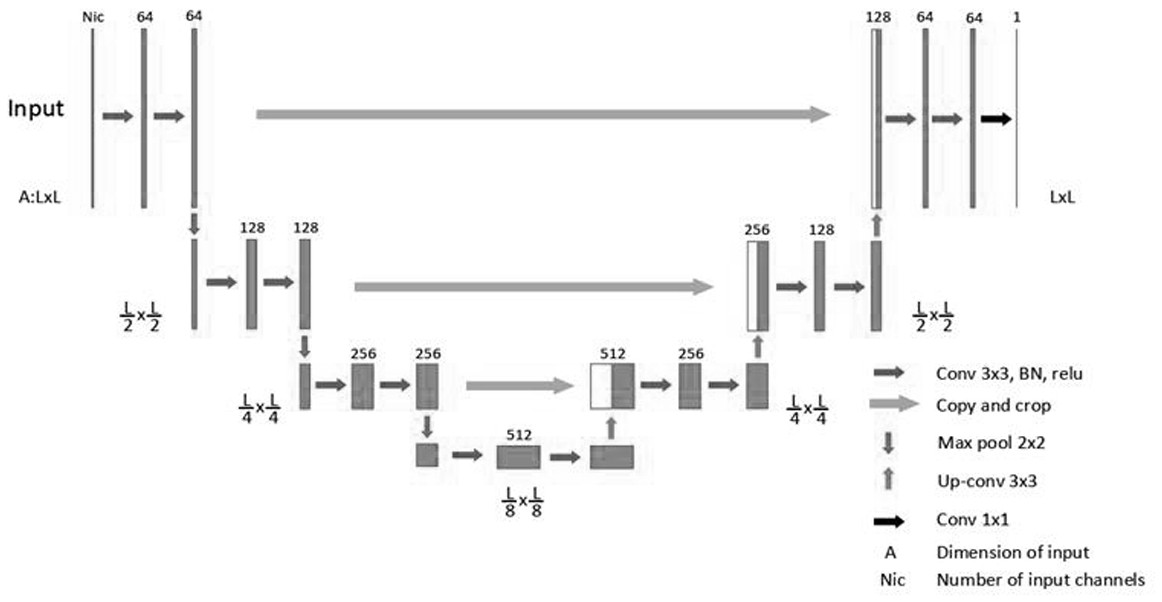
本发明的目的是针对全波数据反演算法和无相位反演算法的优缺点，提出一种基 于基于神经网络解决电磁逆散射问题的两步无相位成像法。所谓的“两步”表示该方法分成 两步实现：第一步是无相位数据处理阶段，目的是将无相位总场数据恢复为散射场数据；第 二步是图像反演阶段，目的是重建出未知散射体的图像。该方法的优势在于避开了直接测 量散射场信息，只需测量无相位总场即可。在得到无相位总场数据后，利用“两步”中的第一 步来将无相位数据恢复为散射场数据，然后利用“两步”中的第二步来重建散射体图像。本 发明需要训练两个不同的CNN的来实现。 本发明的技术方案： 本发明提出分两步来重建散射体图像。第一步是相位恢复，即将无相位总场数据 恢复为散射场数据。第二步涉及到电磁逆散射反演算法。主要内容如下： 一、通过电磁场相关知识得到无相位总场数据与散射场数据： 假定某未知物体存在于自由空间背景下的目标区域 内。通常情况下，逆 散射问题的求解需要将目标区域按照一定规则剖分。假定该目标区域被剖分后的网格总数 为N,每一个网格的位置为rn，n＝1,2,3...,N。而在该区域外侧，安装有发射天线和接收天 线(发射天线位置表示为rp,p＝1,2,…,Ni，接收天线位置表示为rq,q＝1,2,…,Nr)，应用该 设置可获得Ni×Nr个散射场数据。设散射体由非磁性且各向同性的非均匀媒质组成，那么逆 散射成像问题可归结为应用散射场Esca(rq)求解目标区域D内的介电常数分布ε(rn)。 由Lippmann-Schwinger电场积分方程，可以得到总场积分方程： 其中Einc(r)表示位于区域内部r处的入射场；χ(r)＝(ε(r)-ε0)/ε0为区域内的对比 度函数；k0表示自由空间中的波矢；格林函数 表示一个位于 空间r′处的点源对其周围空间某点r所产生的场， 表示零阶第一类汉克尔函 数。 散射场积分方程： 其中Esca(rq)表示位于rq处的接收天线接收到的散射场的信息； 对比源为对比度和总场的乘积，定义为： I(r)＝χ(r)Etot(r)                           (3) 将公式(1)-(3)离散化： 其中 ⊙ 表示对应元素相乘，格林函数 为离散后的格林函数G(rq ,r ')的积分算 6 CN 111609787 A 说　明　书 3/6 页 子， 为离散后的格林函数G(rn,r')的积分算子。把公式(6)计算出来的感应电流代入到公 式(5)中，可以计算得出所需的散射场数据。公式如下： 其中 代表单位矩阵。 无相位总场的定义如下： 其中 表示在无未知散射体时，接收天线接收到的场信息。 二、搭建神经网络： 本发明所使用的神经网络是U-net神经网络。U-net的典型特征是一个“U”形对称 结构网络(如附图2所示)。U-net的左侧是一条收缩路径，它主要由卷积和池化操作组成。左 侧每一层都先经过两次卷积操作。每个卷积都要经过批量归一化(Batch  Normalization， BN)和激活函数(ReLU)处理，BN可以有效地加速深层网络训练。然后是最大池化合并操作进 入下一层，在每个下采样步骤，图片尺寸缩小一半，同时特征通道的数量加倍。U-net的右侧 是一条扩展路径。扩展路径主要用于恢复矩阵，其每个步骤都包括特征图的上采样，然后是 反卷积，将特征通道的数量减半，同时矩阵尺寸增加一倍，用于将矩阵恢复到原始大小。由 U-net的每个卷积层获得的特征图将连接到相应的上采样层，以便可以在后续计算中保留 更多原矩阵的信息。U-net架构最初用于医学分割，它可以很好地预测每个像素的值。 本发明的有益效果是： 本发明主要是针对全波数据反演算法和无相位反演算法的优缺点，提出一种基于 基于神经网络解决电磁逆散射问题的“两步”无相位成像法。在电磁逆散射成像领域，全波 数据反演算法由于具有更多的散射体信息(幅值和相位信息)，比无相位反演算法的非线性 要低，更容易计算。但是全波数据反演算法需要使用具有幅值和相位信息的散射场数据，实 际当中散射场的准确测量却是相当困难。本发明能避开直接测量散射场的方法来得到散射 场信息，并表现出不错的反演效果。 附图说明 图1是测量场信息的实验装置结构图； 图2是U-net结构图； 图3是训练神经网络所用的部分训练样本展示图； 图4a和图4b分别是Austria散射体结构图及反演图； 图5a和图5b分别是FoamDielExt结构图和实测数据FoamDielExt的反演图。