技术摘要:
本发明专利涉及植物叶面积测量领域,提供基于多元正态分布统计和水平集变分法的叶面积自动测量系统,该系统由图像采集系统和图像处理系统组成。图像采集系统主要负责图像采集功能,由带黑色边框的白色矩形背景板、软质透明塑料盖板、夹子和图像采集设备构成。图像处理 全部
背景技术:
叶面积是研究叶片功能、生理生化、作物栽培的重要指标,是估算植物表型特征模 型的重要参数,因此植物叶面积的测量具有十分重用的作用;目前常用的叶面积测量方法 很多包括方格纸法、复印称重法、叶面积扫描仪、图像处理法等,其中方格纸法、复印称重法 测量准确,但操作繁琐,费时费力且需要采摘叶片进行离体测量;叶面积仪测量叶面积精度 高,测量速度快,但价格昂贵,维修费用高,且扩展性差不适用于大面积叶片面积的测量;图 像处理法是利用数码相机或手机拍摄植物叶片和已知面积的参照物,通过计算图像中叶片 像素点个数与参照物像素点个数的比例,从而计算出叶片面积,该方法操作方便,测量速度 快,目前得到广泛应用;但目前常见的基于图像处理的测量装置还存在一定问题:拍照要求 较高,需要采摘叶片进行拍照,无法实现无损测量;图像处理时需将图像二值化后再对其进 行边缘测量和图形分割,分割效果受拍摄条件影响较大,测量精度不稳定。
技术实现要素:
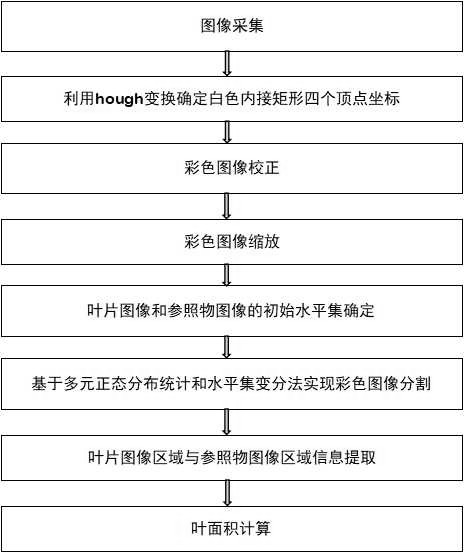
本发明专利针对上述测量方法的不足之处,研究一种基于多元正态分布统计和水 平集变分法的叶面积自动测量系统,利用手机或数码相机拍摄平铺在背景板上的叶片,通 过hough变换实现图像自动校正;且对校正后的彩色图像利用多元正态分布统计和水平集 变分法进行叶片和参照物目标的自动提取,最后通过参照物的实际面积、叶片图像与参照 物图像的像素点个数的比值计算出叶片面积。该测量系统针对彩色图像进行图像分割,自 动计算叶片面积,对拍摄环境、拍摄角度要求较低,测量精度高,且能实现植物叶面积的离 体和非离体测量。 本发明专利通过以下技术方案实现。 叶面积自动测量系统由图像采集系统和图像处理系统组成。 图像采集系统由拍照载物平台和图像采集装置构成,其中载物平台由背景板、软 质透明塑料盖板、夹子组成。为了便于图像校正和叶面积检测,背景板为外围带有黑色矩形 边框的白色硬质木板,白色矩形区域右上侧印制红色方形参照物,红色参照物的面积可根 据测量的叶片大小确定,叶片增大,参照物可相应增大,以减小测量误差。 将植物叶片平铺在背景板白色矩形中间,平铺时不要出现叶片重叠现象,且叶片 不能覆盖红色参照物,也不能超出白色矩形区域;叶片放置好后用软质、透明、反光小的塑 料与夹子相配合将叶片固定可实现植物叶面积的离体和非离体测量,同时也可提高测量精 度。 图像采集时选取光照条件好的环境,图像采集装置选用手机或数码相机,拍照时 4 CN 111553943 A 说 明 书 2/6 页 注意相机视场覆盖整个载物平台,拍照应清晰且防止出现抖动模糊现象。 图像处理系统包括如下步骤。 步骤1;利用网络或存储介质将采集的彩色图像传输到PC端,并利用图像处理软件 MATLAB读取图像。 步骤2:为减小不同拍照角度产生的图像畸变,提高测量精度,本发明专利利用背 景板上黑色边框作为参照,以此确定白色内接矩形的四个顶点来校正拍摄过程中产生的畸 变。具体方法为利用log算子检测图像边缘信息,在此基础上利用hough变换自动查找背景 板上的白色矩形的四条边并确定这四条直线的四个交点(即内部白色矩形的顶点)的坐标 ;根据四条直线构建的四边形的长宽构建新的矩形即校正后 的矩形,设置新的矩形的顶点坐标为 。 步骤3:实现图像校正;几何校正的思想是根据畸变图像的四个顶点坐标 与新的矩形四个顶点坐标 建立一组函数映射关系式,函数映射关系式如式1所示: (式1) 根据上述映射关系式可列出由8个方程组成的具有9个未知参数的方程组,求出9个参 数,从而确定函数映射关系式,对畸变图像的所有坐标进行映射校正,同时在校正过程中采 用双三次插值进行插值,实现失真图像的几何校正。 本发明专利在实现图像几何校正时,将背景板外围的图像去除,仅保留白色矩形 区域内的图像(包括叶片图像和参照图像),从而得到新的校正后的彩色图像用于下一步图 像信息的提取。 步骤4:为提高图像处理速度,将得到的彩色图像进行缩放。 步骤5:本发明专利采用基于多元正态分布统计和变分法水平集的彩色图像分割 方法,该方法曲线演化过程中需要定义初始水平集,具体方法为利用色调信息确定叶片图 像和参照图像的大致区域,在此基础上,随机给出叶片图像和参照物图像的初始水平集。 步骤6:基于多元正态分布统计和水平集变分法方法实现叶片图像、参照物、背景 图像的彩色图像分割。 进一步的,本发明专利的分割思想是:将图像的颜色值看成具有一定概率分布的 随机变量,则图像分割问题可看成基于最大后验概率的优化问题。为此先构建基于区域统 计的图像分割模型,本次图像分割是将图像G分割成3个区域: ,分割能量函数的定义如 式2所示: (式2) 其中, 为区域 中某点像素值 的概率密度,图像分割的目的是当得 5 CN 111553943 A 说 明 书 3/6 页 到图像分割结果时,上式后验分割概率最大。为了应用主动轮廓模型和变分法求解该优化 问题,将式2中的后验概率取负对数 ,引入正则化项 ,将分割能量函 数重新定义如式3: (式3) 因此,将图像分割问题转换为最小化式3所示的能量函数。 选定能量函数后利用水平集表示区域:设 为图像域,用两个水平集函数 和 表示图像分割的三个区域,设 为第i个水平集函数所表示的平面曲线的内部区域, 表 示 平 面 曲 线 的 外 部 区 域 , 表 示 平 面 曲 线 ,即 , , ,则式3中三个区域可表示为: (式4) ,则式3可用水平集 表示为式5: (式5)。 进一步地,最小化式5,对其求偏导,得到如下曲线演化方程: (式6)。 进一步地,为了提高演化速度,将式5中每一项积分区域扩展到整个图像区域,引 入单位阶跃 H e a v s i d e 函数 和单位脉冲D i r a c函数 ,函数定义为 : (式7) 为了简化初始水平集的定义且使水平集在演化过程中不需要再重新初始化,引入约束 项 ,则式5可改写为: 6 CN 111553943 A 说 明 书 4/6 页 (式8)。 利用变分法方法推导欧拉-拉格朗日方程,得到曲线演化方程: (式9) 。 进一步的,实验表明公式9所示演化曲线方程演化速度快,但收敛性差,精度相对 较低,公式6所示演化方程演化速度慢,但收敛性好、精度高。因此本发明专利采用两种演化 方程结合的方式进行分割曲线演化,在步骤5得到的初始水平集的基础上利用公式9所示演 化方程得到叶片和参照物图像的大致轮廓,再通过公式6所示演化方程得到叶片和参照物 图像的轮廓曲线;实验证明这种方法速度快,精度高能满足本发明专利的要求;并且这种分 割方法可根据实际情况调整两种演化方程的迭代次数,方便使用者得到更满意的结果。 为了充分利用图像的颜色信息和颜色特征间的相关性,本发明专利采用多元正态 分布描述各区域内各像素点的概率密度,因此: (式10) 其中, 和 表示第i个区域的特征均值向量和特征间的协方差矩阵。 进一步的,最终的曲线演化可得到三类图像区域,按式4可提取分割结果并按不同 灰度值标记。 步骤7,计算叶面积:已知参照物真实面积为 ,通过步骤6提取图像的叶片区域和 参照物区域信息,统计叶片区域内的像素点个数为 ,统计参照物区域内的像素点个数为 ,则叶片真实面积 可通过公式11计算得到: 。 (式11)。 与现有技术比较,本发明专利的有益效果是:首先本发明专利选用带黑色边框的 白色矩形板及软质、透明、反光小塑料盖板作为拍照平台,一方面可以实现叶片的非离体面 积测量,另一方面可以利用hough变换确定白色矩形的四个顶点坐标来校正由于拍照角度 引起的图像畸变;其次本发明专利采用基于多元正态分布统计和水平集变分法的图像分割 方法实现叶片图像、参照物、背景图像的分割,无需二值化处理,直接对彩色图像进行分割, 边缘轮廓清晰,面积测量精度高;另外本发明专利图像校正及初始轮廓选择均能自动完成, 可移植性强。 7 CN 111553943 A 说 明 书 5/6 页 附图说明 图1为本发明专利叶面积测量方法的流程图。 图2为本发明专利叶面积测量方法拍照背景。 图3为试验叶片图像。 图4为白色内接矩形的四个顶点确定的图像。 图5为图像校正且去除多余背景后的图像。 图6为试验叶片和参照物初始水平集图像。 图7为试验叶片图像分割完成后轮廓曲线图。 图8a为提取出的叶片图像,图8b为提取出的参照物图像。












