技术摘要：
本发明涉及一种多小区场景下的任务卸载和资源分配的联合优化方法，属于移动边缘计算领域。该方法包括：首先，建立多小区场景下的MEC任务卸载模型，并设计系统总开销函数。然后，采用混沌变异二进制粒子群算法来优化用户的卸载决策；在得到用户的卸载决策的情况下，将原  全部
背景技术：
近年来，随着移动互联网与云计算的发展，越来越多的新型应用出现在人们的日 常生活当中，如增强/虚拟现实，人脸识别和交互式游戏等，但由于这些这些新型应用普遍 是计算密集型和延迟敏感型应用，使得移动终端难以有效地执行。虽然移动云计算(Mobile  Cloud  Computing,MCC)能够在一定程度上满足用户对这些应用的性能需求，允许移动设备 将本地复杂、大量的计算任务部分或完全卸载到位于核心网的云数据中心进行执行，从而 解决了移动设备自身资源紧缺问题。但是由于MCC的云数据中心位于核心网，云端和终端用 户的传输距离长，会产生额外的时延开销，不能满足未来低时延高可靠的要求。移动边缘计 算(Mobile  Edge  Computing,MEC)的出现很好地解决了以上问题，MEC是将具有存储和计算 能力的网络设备实体部署在移动网络边缘，从而为移动网络提供IT服务环境和计算能力。 与传统MCC技术中位于核心网的数据中心，MEC更加靠近用户，因此极大地缩短了云计算服 务器与移动设备之间的距离。由此在减少回程拥塞的同时，又大大减少了用户的时延开销。 MEC的关键技术主要包括任务卸载和资源分配两个方面。任务卸载是指将计算密集型或延 迟敏感型任务卸载到资源相对丰富的计算机或服务器中执行，以解决移动设备在存储、计 算等方面存在的缺陷。此外，在多个用户将其各自的计算任务从本地卸载到MEC服务器进行 处理时，涉及到有限的MEC服务器资源在各个用户之间的分配问题，因此，MEC服务器的资源 分配致力于解决移动设备在实现卸载后如何高效公平地分配资源以实现任务处理的问题。 目前在移动边缘计算中存在的主要问题和技术挑战包括： (1)如何制定高效合理的卸载决策。 (2)当用户选择卸载任务时，如何根据有限的无线频谱资源及MEC服务器计算资源 进行合理分配。
技术实现要素：
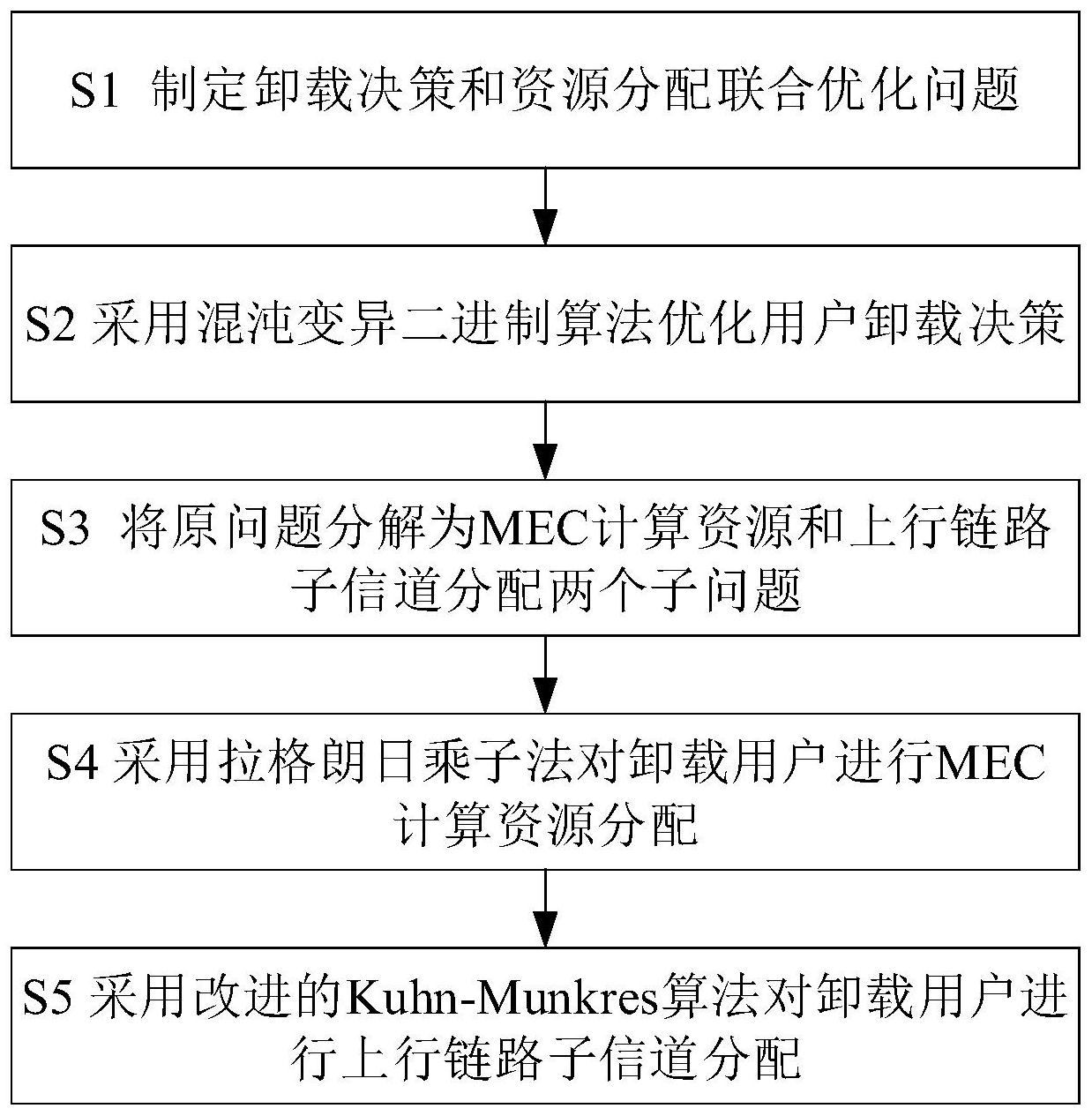
有鉴于此，本发明的目的在于提供一种多小区场景下的任务卸载和资源分配的联 合优化方法。 为达到上述目的，本发明提供如下技术方案： 一种多小区场景下的任务卸载和资源分配的联合优化方法，该方法包括以下步 骤： S1：制定卸载决策与资源分配的联合优化问题； S2：采用混沌变异二进制粒子群算法来优化卸载决策； S3：将原问题分解为MEC计算资源分配和上行子信道分配两个子问题； S4：采用拉格朗日乘子法来对卸载用户进行MEC计算资源分配； 8 CN 111586720 A 说　明　书 2/15 页 S5：采用改进的Kuhn-Munkres算法对用户进行上行子信道分配。 可选的，所述步骤S1具体为： 考虑一个应用MEC的密集异构网络模型，由1个宏基站MBS和J个小小区基站SBS组 成，其中MEC服务器部署在MBS附近，处理由蜂窝网络内卸载至它的任务；各个SBS都以同频 方式部署，并各自与MBS以有线或无线的方式连接；定义SBS集合为 假 设网络中的用户总数为K，定义第i个SBS服务范围内的用户集合记为 其中每个 用户都有计算任务需要执行；定义ak∈{0，1}为用户k的卸载决策，ak＝1表示用户选择将任 务卸载至MEC服务器进行执行，a k＝0表示用户选择在本地设备上进行执行；使用 表示网络中所有用户的卸载决策；将选择卸载计算任务的 用户集合记为 集合的势为 表示其包含的元素个数；将选择本 地执行的用户集合记为 集合的势为 表示用户k选择本地计 算的总开销，即能耗-时延的加权和， 表示用户k选择卸载计算的总开销； 考虑到用户的时延、能耗以及MEC服务器有限计算资源情况下，通过最小化所有用 户 总 开 销 函 数 来 获 得 最 优 的 卸 载 决 策 A * 、M E C 计 算 资 源 分 配 策 略 和上行链路子信道分配矩阵 需要优化的目 标函数为： 其中， 和 分别表示本地和卸载计算时用户k的时延， 表示用户k所能容 忍的最大时延； 表示用户k与相邻SBSj′在上行链路子信道n对应的信道增益，ckn表示子 信道分配情况，ckn＝1表示子信道n被分配给了用户k，否则ckn＝0；fk表示MEC服务器分配给 用户k的计算资源，fmax表示MEC服务器总的计算资源；C1表示用户卸载决策，C2表示计算任 9 CN 111586720 A 说　明　书 3/15 页 务时用户所能容忍的最大时延约束，C3表示用户受到来自其他小小区用户在相同子信道的 干扰不得超过Ith，C4表示MEC服务器的最大计算资源约束，C5表示MEC服务器分配给卸载用 户的计算资源，C6表示卸载用户的子信道分配策略，C7表示同一基站的子信道在一个卸载 周期内仅可以由选定的用户使用一次。 可选的，所述步骤S2具体为： 为防止算法陷入早熟，在粒子群初始化阶段，对粒子位置进行混沌映射优化，将初 始粒子群均匀分布在解空间；同时在每一次迭代更新中利用自适应变异算子将粒子最优位 置进行一定概率的动态变换，然后通过有限次迭代，找到目标函数中的全局最优解；具体步 骤如下： (1)初始化算法参数：惯性权重ω；学习因子c1，c2；种群最大迭代次数T；粒子群规 模I；粒子最大和最小飞行速度Vmax，Vmin以及混沌迭代次数S； ( 2 ) 生成初始化种群 ，粒子 i的位置表示一个可行的 用户卸载决策 ， 采用式(2)进行S次混 沌映射生成一组K个元素的混沌序列初始种群，并利用式(3)对序列中各元素进行{0；1}修 正，以满足二进制编码要求；随机生成粒子i的速度 其中粒 子速度满足 粒子位置进行混沌初始化的过程中，第s次迭代与第s 1次 迭代产生的混沌序列关系为： 其中，yt为第s次迭代产生的粒子位置优化的混沌变量； 表示控制遍历状态的参 数，当 时，系统进入混沌状态，混沌变量能遍历在[0；1]之间的所有状态；为确保混沌 序列元素的值域为[0，1]，使其满足二进制编码方式，选择取整函数对混沌映射后的变量进 行修正；修正公式为： xi＝round(ys 1)                       (20) 其中，round( )算子为取整函数；xi是修正后粒子位置变量； (3)计算初始粒子群的适应值，将公式(1)的目标函数作为适应度函数，取最小值 作为群体当前的最优解，并记录该粒子位置为全局极值点xgb，设定当前每个粒子的位置为 个体极值点xpb；并设置当前迭代次数t＝1； (4)根据式(4)-(6)更新粒子速度、位置，计算粒子的适应度值并更新xgb和xpb； 其中，在式(4)中：ω为惯性权重；c1、c2为学习因子；r1、r2为均匀分布在[0；1]之间 的随机数； 是粒子i的k维位置在第t次迭代中的历史最优位置，简称为个体极值； 是 本代全体粒子的k维位置第t次迭代中的最优位置，称为全局极值；在式(5)中：η是均匀分布 10 CN 111586720 A 说　明　书 4/15 页 在[0；1]的随机数； 是将速度的连续值限制在[0；1]区间内的Sigmoid函数，其表示 式为： 同时，粒子群算法在迭代过程中容易出现早熟收敛；为了让群体快速跳出局部最 优，本发明提出根据公式(7)计算粒子适应度的变化情况，并用来作为早熟的判断条件；假 设第i个粒子的适应度值为δi，整个粒子群的平均适应度为δavg，整个粒子群的适应度方差 为σ2，其表示为： 其中，δ为归一化因子，其表示为： 群体适应度方差σ2反映的是粒子群的变化情况，σ2越小，说明粒子的位置越来越集 中；当σ2＝0时，所有的粒子适应度值相同，说明算法出现早熟或者收敛于全局最优解；本发 明设定一个阈值φ，若σ2<φ，则说明算法出现早熟； 当粒子出现早熟收敛时，提出利用遗传算法中的变异算子来增大粒子的搜索范围 以便跳出局部最优；将粒子局部最优位置以一定的概率进行动态变换以跳出局部最优解， 变异操作表示为： 其中，T表示最大迭代次数，rand表示均匀分布在[0，1]的随机数，mi表示变异概率 因子，mmax表示最大变异概率因子，mmin表示最小变异概率因子，其中mi∈[0.001；0.05]； (5)根据式(7)计算粒子的适应度方差，并判断是否出现早熟收敛；若出现早熟收 敛，则根据变异算子(9)(10)对位置变量进行变异操作； (6)更新粒子的适应度值、每个粒子的个体极值点和全局极值； (7)如果当前迭代次数小于最大迭代次数T，则转到步骤(4)继续向下执行，并将迭 代次数更新为t＝t 1。 可选的，所述步骤S3具体为： 在得出用户的卸载决策后，对原目标函数进行分解，表示为： 11 CN 111586720 A 说　明　书 5/15 页 其中，rkn(ckn)表示用户k的上行链路子信道n的传输速率；pk表示用户k的发送功 率，ζ是设备传输功率放大器的效率，pIdle表示任务在MEC服务器执行时用户在空闲状态下 的功率消耗； 和 表示用户在制定卸载决策时对任务执行能耗和时延的权衡因子；将原 优化问题分为MEC计算资源分配与上行子信道分配两个子问题，且对应分配变量不存在相 互约束，选择对这两个子问题分别进行求解。 可选的，所述步骤S4具体为： 在原问题进行分解后，将计算资源分配问题表示为： 由于g(F)的定义域为凸集，且海森矩阵为半正定，g(F)为凸函数；定义在约束条件 C4，C5下的拉格朗日函数表达式为： 其中，λ和μ分别是与约束条件C3和C4相对应的拉格朗日乘子，且λ，μ≥0；然后根据 KKT条件求得最优计算资源分配 可选的，所述步骤S5具体为： 在特定的卸载决策下，假设用户在各个上行链路子信道的传输功率是相等的；子 信道分配既要满足为用户分配信干噪比大的子信道来最大化用户的上行传输速率，还要尽 可能为每个用户分配相邻小区内占用数量较少的子信道，以尽可能地避免同频干扰；将上 行链路子信道分配问题转化为满足用户最低传输速率与最大可容忍干扰的情况下为用户 分配数量最少的子信道问题，表示为： 12 CN 111586720 A 说　明　书 6/15 页 其中，约束条件C3表示用户k在最大容忍时间 内完成该计算任务所需的最小 传输速率，以Rmin表示，约束条件C4表示用户进行任务卸载时传输速率的约束；将卸载用户 的子信道分配问题转化为Kc个卸载用户与N个子信道的加权二分图匹配问题，采用改进的 Kuhn-Munkres算法进行求解，具体步骤如下： (1)首先构建权值矩阵 矩阵中的每一个元素为卸载用户在此子信道下的 传输速率，表示为： 其中，权值矩阵 中的行坐标表示卸载用户索引，而列坐标表示的是参与分 配的子信道索引； (2)根据步骤(1)中构建权值矩阵的特点，构造二分图G(V1；V2，E；W)；其中，G的上节 点V1表示卸载用户集合；G的上节点V2表示可用子信道集合；边E表示连接两个集合中节点的 边，即卸载用户与子信道的分配关系ckn；权值W表示卸载用户在分配子信道下的传输速率 rkn； (3)由于标准的Kuhn-Munkres算法进行最大权值匹配时，通常要求二分图中的节 点数量相同；对标准Kuhn-Munkres算法进行改进，若卸载用户个数与子信道个数不能完全 匹配，则增加相应的虚拟卸载用户或虚拟子信道节点，从而将权值矩阵进行扩展为 或者RN×N的方阵，其扩展部分的权值取值为0；当Kc>N时，增加Kc-N个虚拟子信道，构 成 方阵；而当Kc