技术摘要：
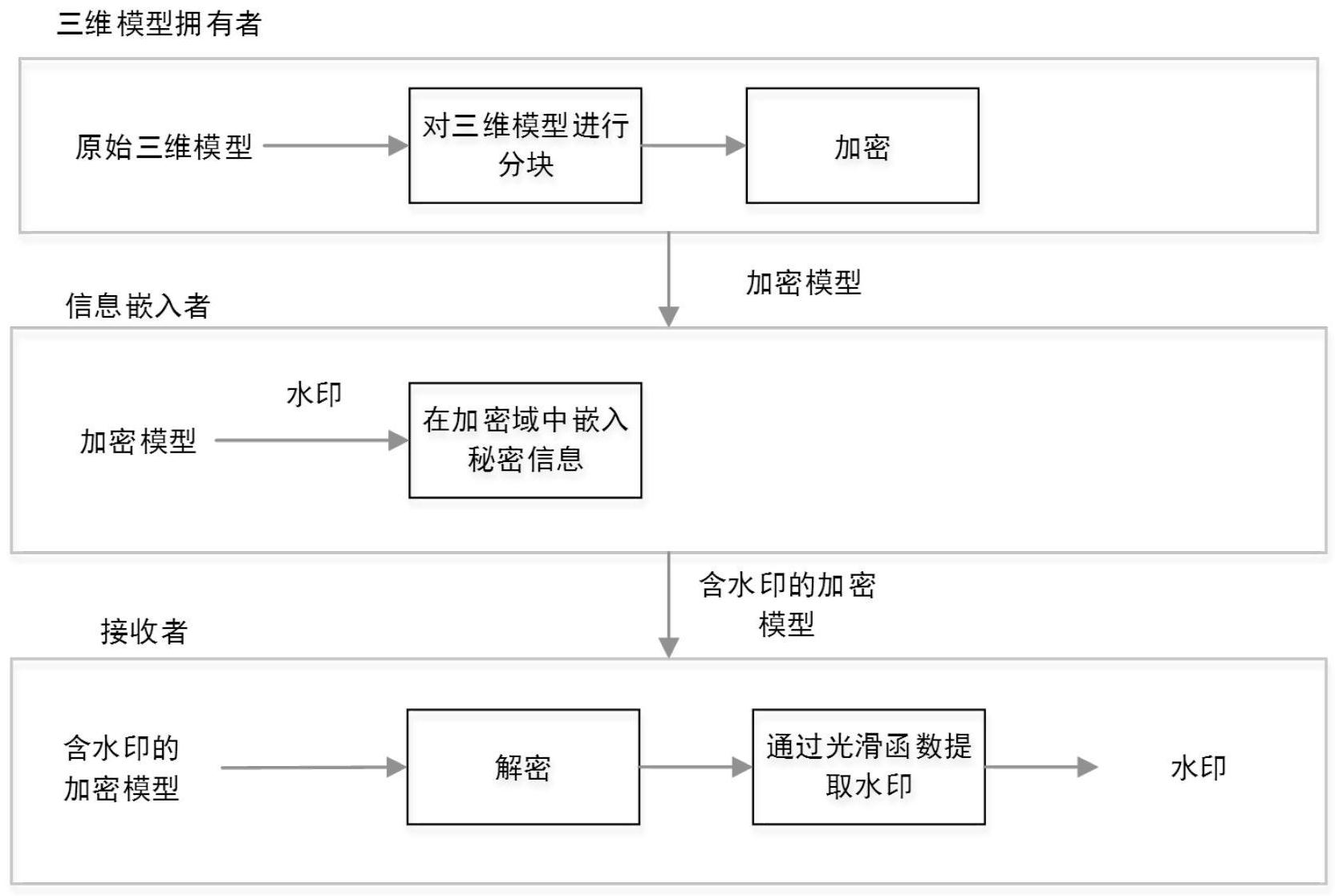
本发明公开了一种基于同态加密域的水印嵌入以及提取方法。针对云平台的数据泄露问题，通过加密系统来实现对上传到云端的三维模型隐私的保护。在传统方法中，由于加密三维模型的不可见性，无法实现三维模型的数据安全性保护。本方法首先将三维模型划分为若干块，并进行  全部
背景技术：
随着三维(3D)模型在网络上的发展，促进了对3D模型的数据安全的相关研究。针 对三维模型的数据安全问题，通常采用嵌入水印的方法。水印主要分为鲁棒水印和脆弱水 印，鲁棒水印可以抵抗对数据载体的攻击，而脆弱水印则用于安全性认证。而针对一些特殊 场合，如医学图像，云计算存储，法律文书图片等，要求嵌入水印后可以无损的恢复原始模 型，因此需要利用可逆水印技术。可逆水印算法主要可以分为以下四大类：无损压缩、差值 扩展、直方图平移以及预测误差扩展。可逆数字水印技术一般不考虑水印的鲁棒性，然而， 含水印的数字多媒体在网络等信道中传输时，不可避免地会遭到各种处理或者干扰，所以， 在许多应用场景中，希望嵌入的水印具有一定的鲁棒性。进几年来，鲁棒可逆水印技术逐渐 成为信息隐藏领域的一个重要的研究方向，已取得一些有意义的成果。 随着互联网技术和云计算技术的快速发展，用户可通过互联网将资料和数据上传 到远程服务器或云端进行存储，当需要时再下载使用。云存储节省了购买设备的开支并提 高了获取资源的便利性。然而，云计算技术在方便人们生活的同时，也引发了数据安全和隐 私保护的问题。因此，在上传到云端之前通常对数据进行加密以提高数据的安全性。同时， 云端管理者希望将一些用户资料相关的信息嵌入到密文数据中实现密文检索和数据保护 等功能。因此，加密域可逆水印技术已经成为近年来大数据云计算背景下信息隐藏领域的 研究热点。 加密域的可逆水印分为两类：“加密前预留空间(RRBE)”，“加密后腾出空间 (VRAE)”。第一种类型在明文域中创建嵌入空间，然后加密预处理的图像。例如，通过将某些 像素的最低有效位(LSB)隐藏到其他像素中，空出的位可以由加密域中的待隐藏值代替。借 助于针对纯文本图像开发的水印方法，提取原始的  LSB值并将其写回，可以准确地恢复原 始图像。另一种方法直接修改加密图像进行数据嵌入。通过加密后的腾出空间，可以更加灵 活地对加密后的图像进行数据隐藏操作。例如，Xiang提出了一种加密域的图像鲁棒水印算 法。首先，将原始图像进行分块并加密。其次，在加密域中计算每个分块的统计量，然后对统 计量直方图进行平移来嵌入水印。
技术实现要素：
随着三维模型在网络上的广泛运用，三维模型的安全性受到极大重视。为了解决 现有技术中存在的问题，保护云计算中三维模型的安全性，本发明提出了一个基于同态加 密域的三维模型鲁棒水印方法。首先，将三维模型划分为若干块，并进行分块加密。其次，利 用Paillier加密系统加法和乘法的同态性，对每个扇形块嵌入水印。最后，由于原始三维模 型具有一定的空间相关性，通过评估块的光滑度提取水印。 5 CN 111598765 A 说　明　书 2/10 页 本发明具体采用的技术方案如下： 一种基于同态加密域的三维模型鲁棒水印方法，其步骤如下： S1：对三维模型进行预处理，使三维模型的取值范围为(-1 ,1)的浮点型顶点坐标 转化为正整数，转化方法为： 其中，vi为三维模型的顶点，vi,j为顶点vi的原始j轴坐标,j∈{x,y,z}；v′i,j为顶点 vi转化后的j轴坐标，k为三维模型显示的有效位数； S2：将S1中获得的三维模型划分为若干扇形块，并保证块之间不重叠，划分方法如 S21～S26所示： S21：利用floyd算法计算三维模型中各个顶点之间的最短距离； S22：初始化扇形块中心顶点集合S为空集，从三维模型中取第一个顶点v1添加至 集合S； S23：统计三维模型中与集合S中所有顶点的距离大于等于3的顶点集合Vj，并执行 S24； S24：判断集合Vj是否为空，若不为空，则将Vj中第一个顶点添加至集合S  中，并重 新执行S23，若为空集，则停止循环； S25：从集合S中选择第一个顶点vi，将顶点vi的一环邻域内所含顶点划分为第l个 扇形块P(l)，扇形块编号l的初始值为1，P(l)中的顶点排序如下，： 式中：P(l)(p)表示排序后的扇形块P(l)中第p个顶点，N 表示扇形块P(l)l 中的顶点 数，vk表示顶点vi的一环邻域内除vi之外的顶点； S26：不断重复S25，依次遍历集合S中的每一个顶点，直至集合S中所有的顶点被遍 历完，将三维模型划分为若干扇形块； S3：利用Paillier加密系统对每个块进行加密，加密过程中对于每个扇形块P(l)， 均需要对其三维坐标分别利用公钥(N,g)进行加密，得到该扇形块对应的密文，加密公式如 下： 式中：j∈{x,y,z}，C(l)(p,j)为加密后的扇形块P(l)中第p个顶点的j轴坐标，E[·] 为Paillier加密系统的加密函数，P(l)(p,j)表示扇形块P(l)中第p个顶点的j轴坐标； S4：通过修改扇形块的密文中第一个顶点的坐标，分别在三维模型的每个扇形块 的密文中依次嵌入1比特位的水印，得到用于发送给接收方的三维加密模型；其中每个扇形 块中的水印嵌入规则为：若当前扇形块P(l)中需嵌入比特0，则不改变P(l)的第一个顶点的坐 标； 若当前扇形块P(l)中需嵌入比特1，则在P(l)的密文中修改第一个顶点的坐标，改变 量为B，修改公式如下： 6 CN 111598765 A 说　明　书 3/10 页 式中： 为Paillier加密后的扇形块P(l)中第1个顶点嵌入水印后的j轴坐 标，C(l)(1,j)为Paillier加密后的扇形块P(l)中第1个顶点的j轴坐标，j∈{x,y,z}； 上述改变量B对应在明文中的修改如下： 式中： 表示扇形块P(l)中第1个顶点嵌入水印后的j轴坐标，P(l)(1,j)  表示 扇形块P(l)中第1个顶点的j轴坐标； S5：接收方在接收到三维加密模型后，先将三维加密模型进行解密，得到三维解密 模型，三维模型解密公式如下: 式中：D[·]为Paillier加密系统的解密函数； S6：针对三维解密模型，再次按照S2中的方法将其划分为若干扇形块，并保证块之 间不重叠； S7：依次针对S6中划分得到的每个扇形块进行水印提取和原始顶点恢复，具体过 程如S71～S73所示： S71：针对扇形块中的第一个顶点Pw，将其三维坐标值去除改变量B，得到顶点Pw可 能的原始顶点Pw1；在扇形块中，保持其他顶点坐标不变，分别计算顶点Pw的高斯曲率G(Pw) 以及顶点Pw1的高斯曲率G(Pw1)； S72：基于S71中得到的两个顶点的高斯曲率，在当前扇形块中提取1比特位的水印 w，提取公式为： S73：根据S72中提取到的水印，恢复当前扇形块中第一个顶点Pw的坐标恢复至原 始顶点P的坐标，公式如下： 在上述技术方案基础上，各步骤可以进一步采用如下优选方式实现。 作为优选，所述的步骤S1中，若三维模型的顶点坐标取值范围不是(-1,1)，则需要 对其进行坐标值转换。 作为优选，所述的步骤S1中，三维模型显示的有效位数k＝4。 作为优选，所述的步骤S21中，计算三维模型中各个顶点之间的最短距离的具体做 法如下： 首先，将三维模型视为加权图，预设矩阵Dis，其中矩阵中第i行第j列的元素Dis (i,j)表示顶点vi到顶点vj的最短路径的距离；初始状态下，若顶点vi与顶点vj相邻，则Dis (i,j)＝1，否则，Dis(i,j)＝∞； 然后，针对三维模型中的每个顶点vk对矩阵Dis进行一次更新；在每一次更新时， 以顶点vk为基准，遍历其余的顶点vi和顶点vj的组合，判断Dis(i,k) Dis(k,j)