技术摘要：
本发明公开了一种双出杆液压缸位置伺服系统的自抗扰鲁棒（RISEESO）控制方法，该方法将基于扩张状态观测器(ESO)的干扰补偿与误差符号积分鲁棒(RISE)相结合，运用Lyapunov稳定性理论证明了系统渐近稳定的结果。所提策略将干扰抑制方法（RISE）与干扰估计补偿方法有效结  全部
背景技术：
液压位置伺服系统凭借其功率密度大，力/转矩输出大，抗负载刚性强等特性，在 飞行器、重型机械、高性能旋转测试设备等领域有着举足轻重的地位。然而，液压系统固有 的非线性特性及各种建模不确定性使得其控制器的设计复杂化。起初大量研究基于线性控 制理论对液压系统进行控制器的设计，如PID控制器，但是线性控制器的设计是基于线性化 的液压系统模型，不能反映其非线性的特性，因此不能获得很好的控制效果。反馈线性化控 制可在控制器的设计中实时补偿液压系统的非线性特性，但是要求系统模型信息完全已 知，与实际应用不符。自抗扰控制(ADRC)由于其需要模型信息较少且可以获得优异的控制 性能使其得到了广泛的应用，其特点是采用了一个扩张状态观测器(ESO)将系统的集成扰 动扩张为一个新的状态变量，将观测的扰动通过前馈补偿的方式作用于系统以提高控制性 能。为了使非线性ESO在实施中得以简化，线性ESO得以提出，在实际控制中，其仅有一个参 数需要调节，因此大大方便了控制器设计与设备调试过程，且理论证明表明状态估计误差 随着观测器带宽的增大而单调减小。在系统的未建模动态较大时，为了使控制精度提升，必 须提高观测器的带宽，然而，过大的带宽会放大系统噪声甚至使系统不稳定。误差符号积分 鲁棒(RISE)控制方法也可以有效地处理建模不确定性的问题，其包含一个独特的误差符号 积分鲁棒项，可以在系统干扰足够平滑有界的情况下获得渐进稳定的跟踪性能。但是该控 制方法所设计的控制器中的非线性鲁棒增益的取值需要满足一定的条件，该条件跟系统的 建模不确定性对时间的一阶导数和二阶导数的上界密切相关，当系统未建模动态较大时， 为了使得控制性能得以优化，必须取较大的反馈增益，同样，这也会使得系统有震荡的风 险。
技术实现要素：
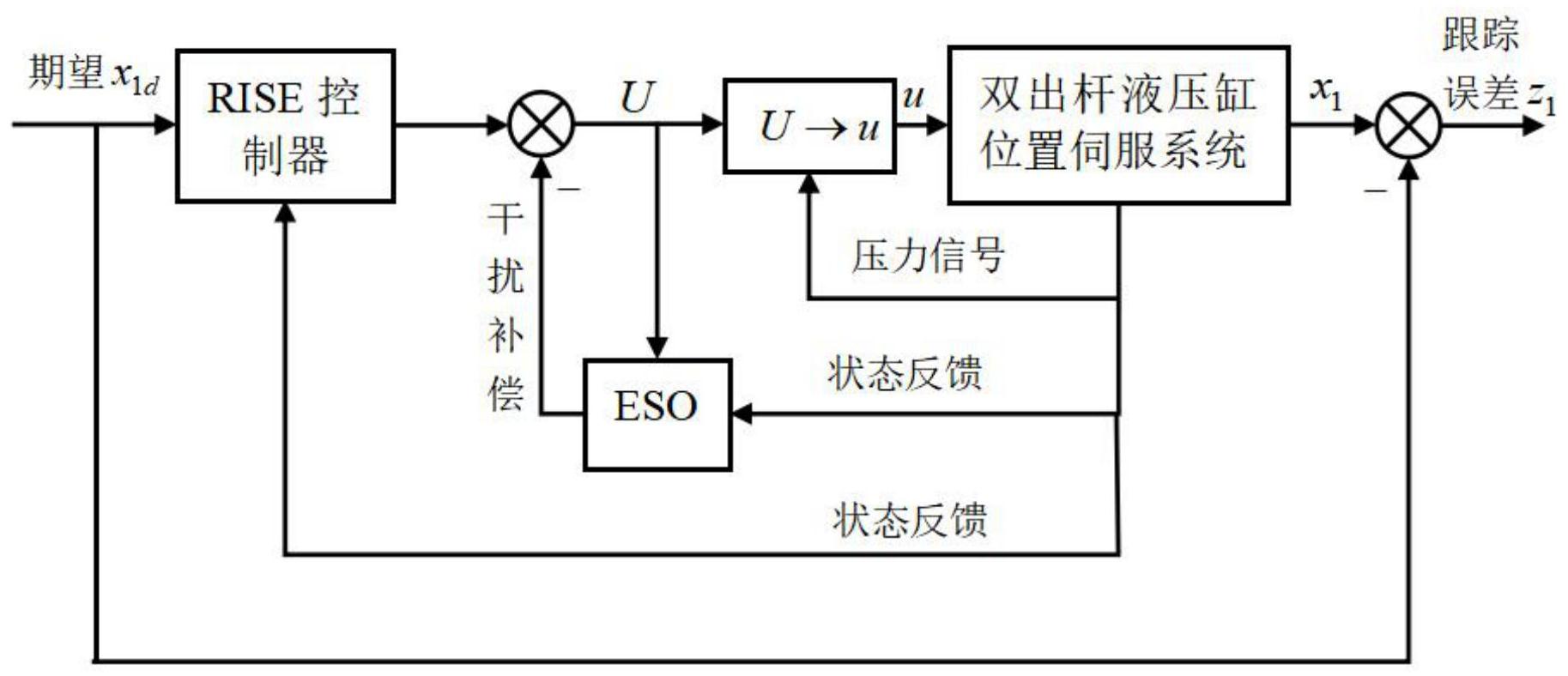
本发明的目的在于提供一种强抗扰、跟踪性能高的双出杆液压缸位置伺服系统的 自抗扰鲁棒控制方法，可以使得双出杆液压缸位置伺服系统拥有较大干扰时仍然保持优秀 的控制性能。 实现本发明目的的技术解决方案为：一种双出杆液压缸位置伺服系统的自抗扰鲁 棒控制方法，包括以下步骤： 步骤1，建立双出杆液压缸位置伺服系统的数学模型； 步骤2，根据上述双出杆液压缸位置伺服系统的数学模型设计自抗扰鲁棒控制器； 步骤3，所述运用李雅普诺夫稳定性理论对双出杆液压缸位置伺服系统进行稳定 性证明，并运用Barbalat引理得到系统能够达到渐进稳定的结果。 本发明与现有技术相比，其显著优点是：将基于干扰抑制(RISE)与干扰估计补偿 7 CN 111577711 A 说　明　书 2/9 页 (ESO)有效结合，RISE的使用进一步减小了ESO的估计残差，使得控制性能得到提升，同时， 改进后RISE的非线性鲁棒反馈增益项仅与状态估计误差的导数相关，比原先的条件更容易 满足，控制器跟踪性能相比传统RISE与ESO都有了改进。仿真结果验证了其有效性。 附图说明 图1是本发明双出杆液压缸位置伺服系统的原理图。 图2是双出杆液压缸位置伺服系统的自抗扰鲁棒控制(RISEESO)方法原理示意图。 图3是双出杆液压缸位置伺服系统期望跟踪的指令信号随时间变化的曲线图。 图4是Case1中RISEESO控制器、RISE控制器、ESO控制器、PID控制器的跟踪性能对 比曲线图。 图5是Case1中RISEESO控制器作用下系统的控制输入示意图。 图6是Case2中RISEESO控制器、RISE控制器、ESO控制器、PID控制器的跟踪性能对 比曲线图。 图7是Case2中RISEESO控制器作用下系统的控制输入示意图。