技术摘要：
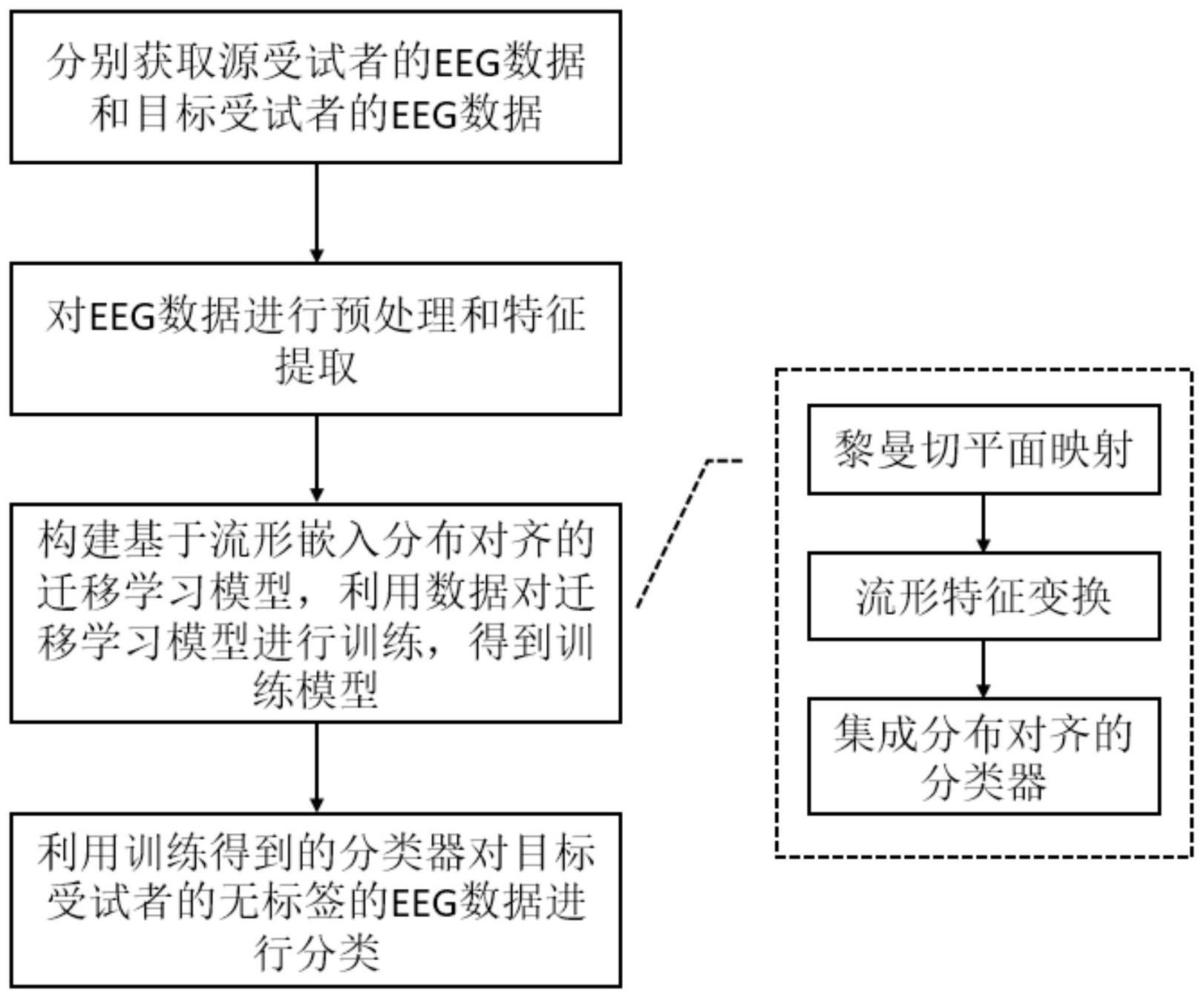
本发明公开了一种基于流形嵌入分布对齐的脑机接口迁移学习方法，包含以下步骤：分别获取源受试者的EEG数据和目标受试者的EEG数据；对EEG数据进行预处理和特征提取；构建基于流形嵌入分布对齐的迁移学习模型，利用数据对迁移学习模型进行训练，得到训练模型；利用训练得  全部
背景技术：
脑机接口(BCI，Brain  Computer  Interface)是通过计算机或其他电子设备在人 脑与外界环境之间建立一条不依赖于外周神经和肌肉组织的对外信息交流和控制通路。它 通过采集脑电信号，经过信号处理将其转化为控制命令传送到外部设备，从而实现人脑的 对外控制。该技术形成于20世纪70年代，是一种涉及神经学、医学、信号检测、信号处理、模 式识别等多个领域的交叉技术。脑机接口目前主要用于医疗康复领域，为那些丧失运动功 能而大脑功能相对完善的患者带来方便。 由于脑电信号存在平稳性较差、信噪比较低的特点，因此脑机接口在实际应用中 需要耗费用户较长的训练时间来产生带标签的训练样本，以训练生成可靠的分类模型，然 后才能投入正常使用。无论对于健康用户还是医疗患者，该枯燥的训练阶段都无疑加重了 他们使用脑机接口产品的负担。迁移学习描述了使用一项任务中记录的数据来提高另一项 相关任务的性能的过程。迁移学习可以应用于在脑机接口中，利用其它用户的脑电图(EEG) 数据来提高当前用户脑机接口中模型的初始性能，减少所需当前用户的训练样本。因此，需 要针对脑机接口系统设计一种有效的迁移学习方法。然而，目前应用于脑机接口的迁移学 习技术存在各种限制条件，最终的效果还不太理想。
技术实现要素：
本发明的主要目的在于克服现有技术的缺点与不足，提供一种基于流形嵌入分布 对齐的脑机接口迁移学习方法，其应用时，可以有效减少脑机接口用户所需的带标签训练 样本。该技术利用其他用户的带标签数据和当前用户的未标签数据，在流形切平面映射和 子空间学习的基础上，把特征分布对齐集成到分类器的训练当中，学习到一个有效的分类 器，可有效提高用于当前用户的脑机接口系统的性能。 本发明的目的通过以下的技术方案实现： 一种基于流形嵌入分布对齐的脑机接口迁移学习方法，包括以下步骤： S1、分别获取源受试者的EEG数据Ds和目标受试者的EEG数据Dt； S2、对EEG数据进行预处理和特征提取； S3、构建基于流形嵌入分布对齐的迁移学习模型，利用数据对迁移学习模型进行 训练，求解模型中的模型参数，从而得到训练后的分类器； S4、利用分类器对目标受试者的无标签的EEG数据进行分类。 在步骤S1中，所述源受试者的EEG数据Ds含有n个试验数据，且该n个试验数据均带 有标签；所述目标受试者的EEG数据Dt含有m个试验数据，且该m个试验数据均不带标签；n≥ 1，m≥1。 5 CN 111723661 A 说　明　书 2/9 页 所述步骤S2，具体为： S21、使用频率带为8-30Hz的五阶巴特沃斯滤波器对EEG信号进行带通滤波； S22、截取用户执行心理任务后的0.5-2.5s产生的EEG信号样本 Xi表示 第i次试验的样本，其中ne表示记录的通道数， 表示实数集，Ts表示采样时间点的数量； S23、对于第i次试验，使用样本协方差矩阵估算空间协方差矩阵： 其中，T表示矩阵的转置。 步骤S3中，所述构建基于流形嵌入分布对齐的迁移学习模型，包括以下步骤： S31、黎曼切平面映射，是指将各个受试者的试验数据集(对应多个空间协方差矩 阵)投影到位于其黎曼均值的切平面上，生成ne(ne-1)/2维的向量si作为接下来流形特征变 换的初始特征： 其中，upper运算符是指保留对称矩阵的上三角部分，并通过对其对角线元素赋予 单位权重，而对非对角线元素赋予 权重从而对其进行矢量化， 表示黎曼均值； 所述黎曼均值，是指使用黎曼测地线距离计算多个协方差矩阵的中心，其计算公 式如下所示： 其中I表示协方差矩阵的数量， 表示协方差矩阵P与Pi的黎曼测地线距离 的平方； 其中黎曼测地线距离定义为 其中F表示Frobenius范数，λi,1...n表示 的特征值； 黎曼切平面映射一方面利用黎曼测地线距离度量协方差矩阵的距离可有效提高 数据域的类别判别性能，另一方面向黎曼中心所在切平面投影得到的向量特征使得源域和 目标域数据的中心点均为零，一定程度上减小了两个数据域的差异。 S32、采用GFK(Geodesic  Flow  Kernel)方法进行流形特征变换：将源数据集和目 标数据集嵌入到Grassmann流形中，然后，在两点之间构造一个测地线流，并沿流Φ积分无 限个子空间； 具体而言，将原始特征投影到这些子空间中以形成无限维特征向量；这些特征向 量之间的内积定义了一个内核函数，该函数能够以封闭形式在原始特征空间上进行计算； 内核封装了子空间之间的增量更改，这是两个域之间的差异和共同点的基础。因此，学习算 法使用该内核来推导对域不变的低维表示； 6 CN 111723661 A 说　明　书 3/9 页 同时，流形空间中的特征能够被表示为z＝g(s)＝Φ(t)Ts，其中g表示流形变换函 数，Φ(t)表示两点之间的测地线，s为黎曼切平面映射得到的特征；变换后的特征zi和zj的 内积定义了一个半正定的测地线流式核： 其中G表示变换函数； 原始空间的特征可以转换到Grassmann流形中： S33、集成分布对齐的分类器，是以结构风险最小化原则和正则化理论为基础的迁 移学习框架；具体而言，该分类器模型旨在优化以下三个目标函数： 1)最小化源域标记数据Ds上的结构风险函数； 2)最小化联合概率分布Js和Jt之间的分布差异； 3)最大化边际分布Ps和Pt背后的流形一致性。 令预测函数(即分类器)表示为f＝wTφ(z)，其中w是分类器参数，φ:z  a 是把原 始特征向量投影到希尔伯特空间 的特征映射函数；采用平方损失，f可公式化为 其中K是φ导出的核函数，使得＜φ(zi) ,φ(zj)＞＝K(zi,zj)，并且σ、λ和γ是正 则化参数，式中其余参数含义如下文所述； 所述源域标记数据Ds上的结构风险函数是指： 其中 是核空间中的一组分类器， 是 中f的平方范数，σ是收缩正则化参 数，(yi-f(zi))2是平方损失函数； 所述最小化联合概率分布Js和Jt之间的分布差异，是指同时最小化边缘分布Ps和 Pt之间的分布距离和条件分布Qs和Qt之间的分布距离： 其中Df ,K(Ps ,Pt)为边缘分布Ps和Pt之间的分布距离， 为条件分布 Qs和Qt之间的分布距离，C是类别个数；采用投影最大均值差异MMD作为距离度量来度量分 布距离；通过用联合分布适应对结构风险进行正则化，在 中的边际分布和条件分布的样 本矩都被拉近了。 所述最大化边际分布Ps和Pt背后的流形一致性，是指在测地光滑度下，流形正则 化为 7 CN 111723661 A 说　明　书 4/9 页 其中Wij是图亲和度矩阵W第i行第j列的元素，Lij是规范化图拉普拉斯矩阵L第i行 第j列的元素； 通过用流形正则化对结构风险进行正则化，能够充分利用边际分布来最大化f的 预测结构与数据的固有流形结构之间的一致性；这能够基本匹配域之间的判别超平面； 该分类器的学习算法如下： 为了有效地求解优化问题，使用如下的表示定理： 其中K是由φ导出的核，αi是系数，w是权重； 利用上述的表示定理重新表示上述三个目标函数，得到最终的目标函数： 其中Y是标签矩阵，K是核矩阵，E是对角标签指示矩阵，M为MMD矩阵。 对目标函数求导，并令导数为0，可得 α＝((E λM γL)K σI)-1EYT， 其中I是单位矩阵。 所述步骤S4，具体为：根据步骤S33中求得的K和α计算得到目标受试者的无标签的 EEG数据的分类输出f(z)，最终的预测标签即为分类输出中最大值对应的标签类别。 本发明与现有技术相比，具有如下优点和有益效果： 本发明使用协方差矩阵作为数据的初始特征，通过黎曼测地线距离来准确衡量协 方差矩阵之间的距离，可以获得较高精度的分类识别，且经过黎曼切平面投影后初步减少 源受试者和目标受试者地EEG数据之间的差异。之后结合子空间学习中的流形特征变换进 一步减少分布差异，同时降低特征维数。最后，把分布对齐集成到分类器的训练中，提高了 目标受试者脑机接口EEG数据的分类准确率。综上所述，本发明利用其他受试者的带标签数 据和当前受试者的无标签数据，结合EEG数据本身特征，通过先进的迁移学习技术有效地提 高了针对当前受试者的脑机接口系统的分类性能，在一定程度上减少了当前受试者的负 担。 附图说明 图1是本发明所述一种基于流形嵌入分布对齐的脑机接口迁移学习方法的流程 图； 图2为本实施例中采用的三种方法在BCI  CompetitionIV-2a数据集上的分类准确 率的示意图。