技术摘要：
本发明提出了一种磁悬浮控制力矩陀螺框架速率伺服系统及控制方法，系统包括速率环控制器、电流环控制器、驱动、力矩电机、电机端光电码盘、谐波减速器、负载端光电码盘、负载、谐波减速器非线性传输力矩模型计算模块与补偿模块。其中谐波减速器非线性传输力矩模型计算  全部
背景技术：
控制力矩陀螺(CMG)和惯性动量轮(IMW)是航天器主要的惯性执行机构。其中，磁 悬浮控制力矩陀螺具有输出扭矩大、动态性能好、控制精度高等优点，是航天器姿态控制的 首选执行机构。框架伺服系统是磁悬浮控制力矩陀螺的重要组成部分，其角速率控制精度 对输出力矩精度有重要的影响。 由于大力矩输出的要求，谐波减速器就成为了磁悬浮控制力矩陀螺进行力矩放大 和传动的良好选择。尽管谐波减速器具备了结构简单、传动效率高、精度高和传动比大等优 点，但是其非线性力矩传输特性也严重影响着其传动性能，尤其是对于具有高精度要求系 统。然而由于磁悬浮控制力矩陀螺本身体积和重量等的限制，无法安装力矩传感器，因此对 谐波减速器的非线性力矩传输特性的建模就显得尤为重要。目前国内外针对谐波减速器非 线性力矩传输特性的建模较少，且多集中在对谐波减速器各个独立行为的分解建模，使得 建模过程繁琐、参数配置复杂；国外有人采用拉格朗日方程等方法对谐波减速器整体进行 建模，但未能考虑柔轮中的弹性势能，使得建模精度较低。
技术实现要素：
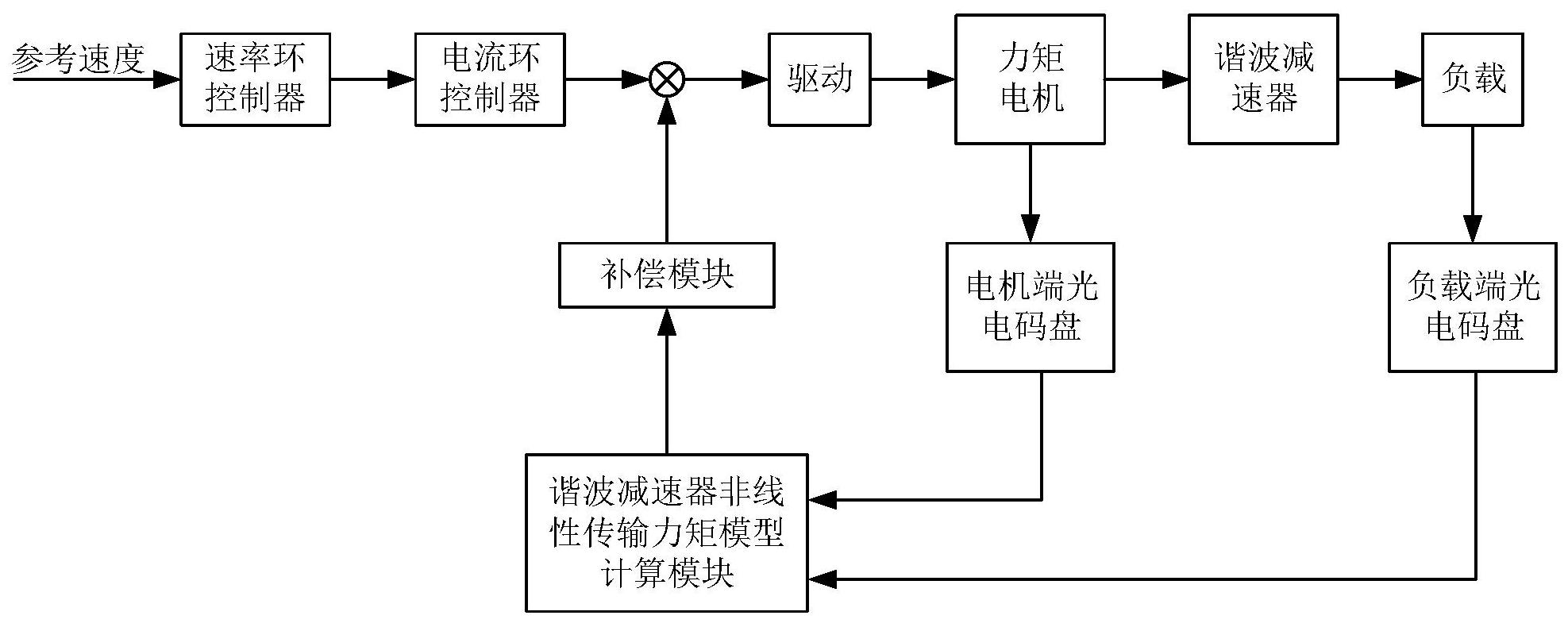
本发明要解决的技术问题是：克服现有磁悬浮控制力矩陀螺框架系统角速率伺服 精度低的问题，给出了框架系统内谐波减速器输出力矩不可直接测量的解决方案，本发明 提供了一种基于谐波减速器非线性传输力矩模型的磁悬浮控制力矩陀螺高精度框架速率 伺服系统，所建系统有利于减小由谐波减速器非线性力矩传输特性而带来的对于框架系统 角速率输出精度的影响。 本发明的基本原理是：本发明在磁悬浮控制力矩陀螺框架伺服系统的基础上，加 入了谐波减速器非线性传输力矩模型的构建与补偿，其中谐波减速器非线性传输力矩模型 是通过建立系统的摩擦模型并进行参数辨识，然后对系统内各能量进行分析，通过运用能 量守恒定律等，推导得到了传输力矩模型；补偿模块则通过将模型计算出的力矩值与实际 期望力矩值的差别补偿到电流环控制器输出的信号中，可以降低由于谐波减速器非线性力 矩传输特性带来的不良影响，明显提升框架系统的角速率伺服精度。 本发明的技术方案是：一种磁悬浮控制力矩陀螺框架速率伺服系统，包括： 速率环控制器、电流环控制器、驱动模块、力矩电机、电机端光电码盘、谐波减速 器、负载端光电码盘、负载、谐波减速器非线性传输力矩模型计算模块、补偿模块； 所述速率环控制器、电流环控制器、驱动模块、力矩电机、谐波减速器、负载、依次 6 CN 111572818 A 说　明　书 2/9 页 连接；所述电机端光电码盘固连到力矩电机转子轴上，所述负载端光电码盘固连到负载旋 转轴上，电机端光电码盘和负载端光电码盘的信号输出到谐波减速器非线性传输力矩模型 计算模块进行计算，其计算结果输出到补偿模块；补偿模块的输出连接到电流环控制器的 输出端； 所述系统的参考速度由姿态控制计算机设定，由速率环控制器计算出相应的电流 值作为参考指令输出到电流环控制器，电流环控制器运算得到电流值对应的信号并输出到 驱动模块，驱动模块输出实际控制电流对力矩电机进行驱动，固连于力矩电机轴上的电机 端光电码盘测量出电机端角位置，同时电机轴另一端与谐波减速器的波发生器固连，谐波 减速器作为力矩放大与传动装置，输出力矩作用在负载上，与负载固连的负载端光电码盘 可以测量出负载端的角位置，将电机端和负载端角位置输入到谐波减速器非线性传输力矩 模型计算模块中，得到模型估计的力矩值，将该估计的力矩值输出到补偿模块并与实际期 望的力矩值进行比较，得到由于谐波减速器非线性力矩传输特性导致的力矩波动量，将该 波动量补偿到电流环控制器输出的信号中，对谐波减速器非线性力矩传输特性不良影响进 行补偿。 本发明还提出一种磁悬浮控制力矩陀螺框架速率伺服系统的控制方法，包括：对 整个伺服系统建立物理模型如下： 由力矩电机产生的输出力矩为Tm，力矩电机的电机转子通过一根刚性轴固连到谐 波减速器的波发生器轴心，该刚性轴受到阻尼系数为Bm的阻尼作用，电机转子、刚性轴及波 发生器的总转动惯量为Jm；波发生器与一柔轮传动连接，波发生器与柔轮间存在减速比为N 的反向传动，柔轮输出侧经过一个弹性系数为K的非线性扭簧将传输力矩Tl作用在输出侧 刚性轴上，该输出侧刚性轴受到阻尼系数为Bl的阻尼作用并固连到负载上，负载及负载侧 刚性轴的总转动惯量为Jl；电机侧和负载侧均受到摩擦力矩的作用； 认为波发生器外壁与柔轮内壁不发生相对位移，谐波减速器两侧所产生的扭转角 仅由柔轮所发生的弹性形变引起，即由物理模型中的非线性扭簧部分的扭转产生，扭转角 表达为： Δθ＝θm/N-θl 其中，θm和θl分别为电机端和负载端角位置。 进一步地，建立谐波减速器非线性传输力矩模型的步骤如下： 步骤(1)：建立基于谐波减速器的磁悬浮控制力矩陀螺框架伺服系统所受摩擦力 矩的模型； 步骤(2)：对所建立的摩擦力矩的模型进行参数辨识； 步骤(3)：对基于谐波减速器的磁悬浮控制力矩陀螺框架伺服系统中输入的能量、 动能、势能、瑞利损耗函数及摩擦力所导致的能量损耗进行分析并得到其表达式； 步骤(4)：根据能量守恒定律，得到谐波减速器非线性传输力矩模型表达式； 步骤(5)：通过实验进行参数校正，并得到最终的谐波减速器非线性传输力矩模型 表达式。 进一步地，所述步骤(1)具体包括： 建立基于谐波减速器的磁悬浮控制力矩陀螺框架伺服系统所受摩擦力矩的模型： 7 CN 111572818 A 说　明　书 3/9 页 其中，Tfm和Tfl分别表示电机侧和负载侧所受到的总摩擦力矩，sign(*)为取符号 函数， 和 分别表示电机端和负载端角速度，Qm和Ql为用于补正电机侧和负载侧摩擦模 型的常数，fcm和fcl分别表示电机侧和负载侧所受到的库仑摩擦力，其表达式为： 其中，am、cm、dm、gm0、gmk、hmk、al、cl、dl、gl0、glk和hlk为库仑摩擦模型中待辨识的参 数，且k＝1,2,…,6。 进一步地，所述步骤(2)具体包括： 在给定参考速度恒定且运行一段时间之后，磁悬浮控制力矩陀螺框架伺服系统将 处于近稳态状态，在该状态下进行实验以辨识摩擦模型所需的参数，参数辨识的方法如下： 在系统空载的近稳态状态下，有： Tm的表达式中只有一项与电机端角速率大小有关，即 因此，首先在同一给定 参考速度的近稳态状态下的多个角位置θm1,…,θmn处进行Tm值的测定，其中n为选取的角位 置的个数，在数字控制系统能够满足条件的情况下使n尽量大，得到n组Tm值；进而多次改变 给定参考速度并使系统达到近稳态状态后，在相同的角位置θm1,…,θmn处进行Tm值的测定， 并且认为不同给定参考速度下相同角位置处的Tfm值相同，对得到的数据进行处理，可以解 得多组Bm的值，适当剔除这多组值中包含的差异较大的值，然后取平均，将得到的平均值作 为真实的Bm值；可选地，若每组Bm值随角位置的波动较大，将Bm建模为角位置θm的函数。 所述Tm值的测定根据下式进行： Tm＝KmI 其中Km是力矩系数，可以通过查阅电机说明书得到；I为电机电流，可以通过电流 传感器实时测得； 得到Bm值后，根据式 测得在同一给定角速度的近稳态状态下电机旋 转整周的Tfm曲线；对该曲线进行滑动平均滤波可以得到Tfm的平均值曲线，对该平均值曲线 采用抛物线近似，即近似为fcm中所包含的多项式 就得到了参数am、cm和 dm的值；然后在不同给定角速度的近稳态状态下采用同样的方法进行多次测量并得到多组 am、cm和dm的值，适当剔除其中差异较大的值后取平均，将得到的结果作为参数am、cm和dm的 真实值； 在上述电机旋转整周的Tfm曲线上减掉Tfm的平均值曲线，可以得到具有周期性波 动的Tfm周期项曲线，通过6阶傅里叶级数对该曲线进行近似，即近似为fcm所包含的多项式 8 CN 111572818 A 说　明　书 4/9 页 其中的系数gm0,…,gm6和hm1 ,…,hm6通过数值积分 获得： 其中，fcm_p(θm)表示在角位置为θm时Tfm周期项曲线对应的值，k＝0,1,…,6； 在系统空载情况下根据以上参数辨识方法即可得到参数Bm、am、cm、dm、gm0、gmk和 hmk，其中k＝1,2,…,6；采用类似的方法在系统带负载的情况下即可得到参数Bl、al、cl、dl、 gl0、glk和hlk，其中k＝1,2,…,6；而Qm与Ql的值则根据具体的实验结果进行调整，在Tfm的平 均值曲线和周期项曲线与其对应模型近似程度较高的情况下，Qm与Ql的值可以取为0。 进一步地，所述步骤(3)具体包括： 将基于谐波减速器的磁悬浮控制力矩陀螺框架伺服系统输入的能量E表示为： 系统的总动能T表示为： 由于框架速率伺服系统各部分始终处于同一面内，不存在重力势能的变化，因此 系统的势能V仅包含柔轮中储存的弹性势能，将其表示为： 又根据胡克定律，可得： 系统的瑞利损耗函数R为： 由于摩擦力导致的能量损耗F可以表示为： 由于谐波减速器的复杂性，除上述能量损耗以外，系统将存在其他较小的能量损 耗，如加工精度与安装误差等导致的齿轮碰撞等会引起能量损失，将其表示为Fc。 进一步地，所述步骤(4)具体为： 根据能量守恒定律可以得到： E＝T V R F Fc 将步骤(3)中得到的各表达式代入，得到谐波减速器非线性传输力矩Tl的模型为： 9 CN 111572818 A 说　明　书 5/9 页 将其离散化，得到： 其中j＝0,1,2,…和i＝0,1,2,…表示采样次数，*j和*i则分别表示在第j次和第i 次采样时*对应的值，*代表公式中的Tm，Tfm，θm，Bm，Tl，Tfl，θl，Bl，Fc等。 进一步地，所述步骤(5)具体包括： 令Fcj＝0，并将上述离散化模型应用到实际的基于谐波减速器的磁悬浮控制力矩 陀螺框架伺服系统的数字控制系统中，输出由模型计算得到的力矩Tl的值，同时通过力矩 传感器实时测得真实输出力矩Tl_ture的值，两者作差得到模型误差曲线，如果模型误差较 大，可以通过对参数Qm和Ql的再调整以及对Fc的整定来进行校正，其中Fc可以设计为常数或 与位置有关的函数；如果模型误差较小，参数Qm、Ql和Fc可以取0； 将Fc取为0，得到最终的谐波减速器非线性传输力矩模型为： 其离散化形式为： 离散化形式可在转化为程序语言后应用于数字控制系统，即谐波减速器非线性传 输力矩模型计算模块。 本发明与现有技术相比的优点在于： 1、现有技术多采用安装力矩传感器或应变片等的方式测量谐波减速器输出力矩， 而本发明在不增加传感器的情况下实现了对于谐波减速器输出力矩的估计。 2、现有技术中对谐波减速器的建模多是对其各个行为的独立建模，这将导致模型 被复杂化且参数配置困难，而本发明则是在建立了系统摩擦模型的基础上从能量角度对谐 波减速器的能量传递和转换的整体行为进行建模，并且考虑了柔轮的弹性势能，在降低模 型复杂性的同时，提高了模型的精度。 3、现有谐波减速器非线性力矩传输模型中多包含角加速度等项，由角位置经过两 次差分后得到的角加速度会含有更多的噪声，而本发明中的力矩传输模型不包含角加速度 项，只有角位置和角速度项，提升了应用方便性的同时提高了应用精度。 附图说明 图1为基于谐波减速器非线性传输力矩模型的磁悬浮控制力矩陀螺高精度框架速 率伺服系统框图； 图2为磁悬浮控制力矩陀螺框架伺服系统简化物理模型图； 图3为谐波减速器非线性传输力矩模型建立流程图。 10 CN 111572818 A 说　明　书 6/9 页