技术摘要：
本发明公开了一种基于ARIMA滤波器的SAGE信道参数估计方法，包括以下步骤：信道参数初始化；初始化漫散射分量的ARIMA滤波器，使用测量数据减去初始化时估计得到的可视距分量和强反射/散射分量，从而对漫散射分量进行初始化；建立漫散射分量的ARIMA模型；基于漫散射分量  全部
背景技术：
由于无线信道具有动态特性，因此无线传输环境中信道参数时刻变化。随着无线 通信技术的发展，人们对无线通信质量的要求越来越高。为了提高无线信道的通信质量，保 证信号有效传输，我们需要对信道参数进行快速准确的估计，因此对高效精确的信道参数 估计方法进行研究具有重要的意义。 近年来，为了对入射平面波的信道参数如：复振幅、时延、入射角、离开角、多普勒 频率等进行估计，有很多高精度的参数估计方法不断提出，如：ESPRIT，MUSIC，Capon的最小 方差法，空间交替期望最大化(Space  Alternating  Generalized  Expectation,SAGE)等。 其中，SAGE算法是一种高效的迭代算法，该算法目前应用较为广泛。该算法可将多维的估计 问题分解为多个一维的估计问题，能够联合的估计出多个多径信号的各个参数且不局限于 收发天线的阵列结构。 现有的方法大多数都是直接使用SAGE算法或改进SAGE算法对测量信号的可视距 (LOS)分量和强反射分量的路径参数进行估计，但是由于原始的测量信号中含有很多漫散 射分量，这些漫散射分量会对信号参数估计产生影响，从而导致SAGE算法有时无法达到全 局最优，不能得到准确信道参数。针对该问题，文献[A .T .Jost ,W .Wang ,D .Shutin ,and  F .Antreich“, Using  an  autoregressive  model  for  DMC ,”in  2012  6th  European  Conference  on  Antennas  and  Propagation(EUCAP) ,March  2012,pp.3504–3508]提出将 AR与SAGE算法相结合提高SAGE算法信道估计结果。该文献利用直接利用AR模型建立漫散射 分量的模型，但是估计的可视距分量、强反射分量及漫散射分量不够准确。
技术实现要素：
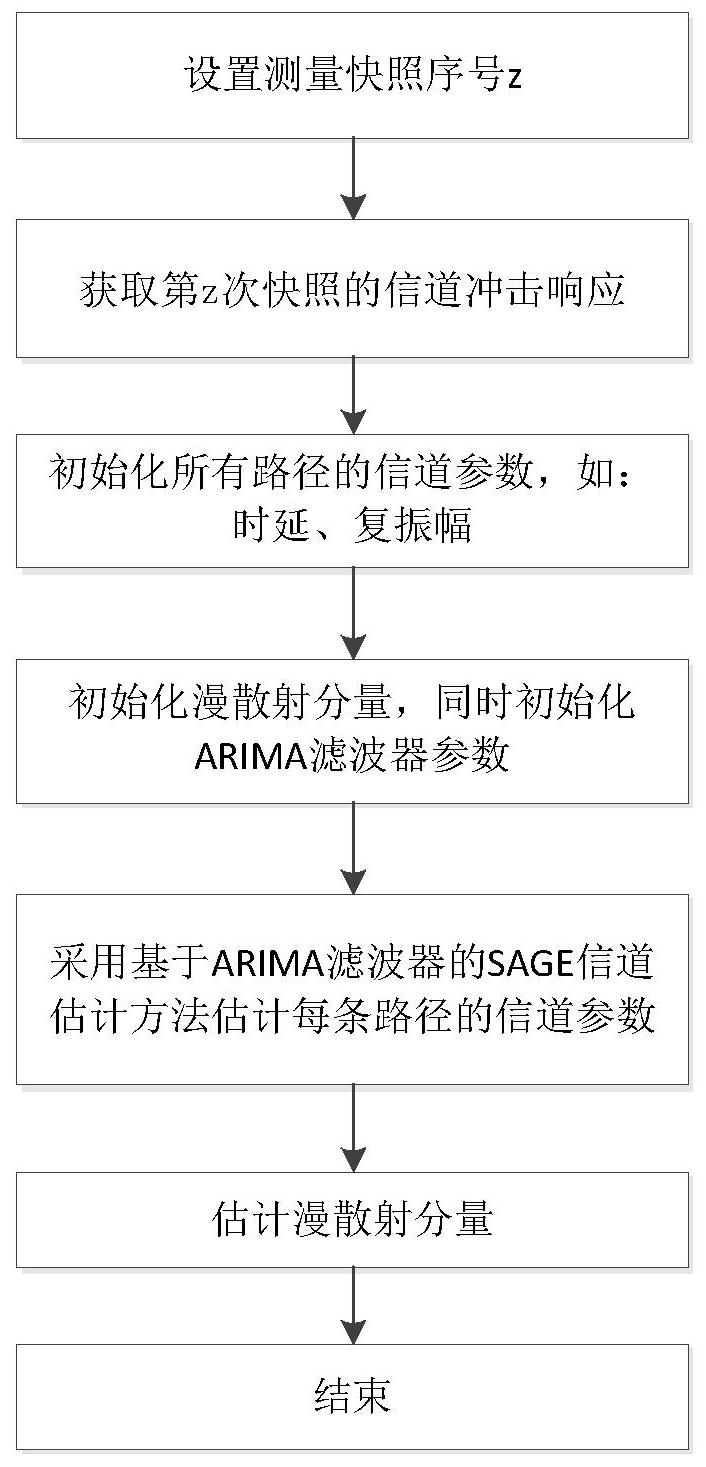
为了解决现有技术中存在的问题，本发明提供一种基于ARIMA滤波器的SAGE信道 参数估计方法，采用ARIMA来建立漫散射分量的模型，而且基于该模型建立ARIMA滤波器。利 用ARIMA滤波器可以从测量信号中过滤掉漫散射分量，剩余信号多为强反射分量，这样可以 更准确的估计出强反射分量的信道参数，从而实现信道参数的更优估计。 为了实现上述目的，本发明采用的技术方案是：基于ARIMA滤波器的SAGE信道参数 估计，包括以下步骤： S1，初始化所有路径的信道参数，具体包括每条路径的时延和复振幅； S2，基于S1初始化的信道参数，计算初始漫散射分量，并基于所述初始漫散射分 量，建立漫散射分量的ARIMA模型，基于漫散射分量的ARIMA模型，建立ARIMA滤波器； S3，基于S2所得ARIMA滤波器，对测量信号进行滤波处理，然后使用SAGE算法基于 滤波后的信号进行迭代优化，估计每条路径的信道参数，每迭代一次，对ARIMA滤波器的参 4 CN 111600665 A 说　明　书 2/5 页 数也进行更新； S4，估计漫散射分量。 S2中，计算初始漫散射分量具体如下： 使用测量的信道频域响应减去初始化时估计的LOS分量和强反射分量，得到的剩 余信号记为漫散射分量；该处估计得到的漫散射分量为初始漫散射分量； 初始漫散射分量为： 其中， 信道频域响应；fm为频率。 S2中，建立漫散射分量的ARIMA模型为： 其中，s(n)为线性系统第n个时间序列，s(n-g)为线性系统第n-g个时间序列；v(n) 为第n个输入序列,v(n-w)为第n-w个输入序列；p为自回归项数，即AR的阶数；q为滑动平均 项数；ag、bw分别为AR模型和MA模型的系数；根据AR模型及MA模型的系数初始化ARIMA滤波 器。 S2中，确定漫散射分量的ARIMA模型具体如下： (1)判断漫散射分量序列是否平稳，若序列平稳，则直接确定AR模型和MA模型的阶 数，并计算AR模型和MA模型的参数；若序列非平稳，则对非平稳的漫散射分量序列数据进行 差分处理，得到差分阶数d，将其转换为平稳序列，然后确定AR模型和MA模型的阶数。 (2)确定ARIMA模型的参数； 采用ACF检验或ADF单位根检验方法，判断漫散射分量序列是否平稳，根据AIC准 则、SC准则或FPE准则确定AR和MA的阶数。 S3具体包括以下步骤： (1)设置迭代次数T的初始值为1；迭代的次数的最大值或估计误差小于设定值err 作为迭代终止条件； (2)设有L条路径，将路径序号i初始值设置为1，最大值设置为L； (3)使用SAGE-ARIMA算法估计第i条路径的时延和复振幅； 基于ARIMA滤波器从待测量信号中过滤掉漫散射分量，留下强反射分量，对过滤之 后的测量信号进行参数估计； 首先，计算第i条路径的条件期望；然后，计算第i条路径的似然函数，通过使第i条 路径的似然函数最大化，得到第i条路径的估计参数，即时延和复振幅； (4)路径序号更新为i 1；判断此时路径序号是否等于L，若等于L则进行下一步；反 之，跳至步骤(3)； (5)基于步骤(3)计算得到的每条路径的估计参数，重新计算漫散射分量，并更新 ARIMA滤波器的时延和复振幅； (6)根据迭代次数是否达到最大值或迭代结果是否收敛，判断是否终止迭代； 若迭代次数T达到最大值或第T次的迭代结果与第T-1次的迭代结果的差值小于误 差值0.000001，则跳出迭代循环，当前测量快照的信道参数估计结束；若迭代次数小于等于 5 CN 111600665 A 说　明　书 3/5 页 设定值且迭代结果的差值大于设定值err，则迭代次数T加1，跳至步骤(1)继续进行。 S4具体如下： (1)根据S3得到的信道参数复振幅和时延，重构估计的可视距分量和强反射分量 信号 (2)使用实际测量的信道频域响应数据减去重新估计得到的可视距分量和强反射 分量得到估计的漫散射分量； 其中， 信道频域响应；fm为第m个频带的频率。 与现有技术相比，本发明至少具有以下有益效果： 本发明首先基于漫散射分量建立ARIMA滤波器，然后过滤掉信号中的漫散射分量， 最后估计多径信号的参数，采用本发明所述方法，已经提前过滤掉了信号中的漫散射分量， 剩下的信号多为可视距分量或强反射分量，使用SAGE算法进行信道参数估计可以减小漫散 射分量对参数估计的影响，可以更快、更准确的估计出可视距分量或强反射分量的路径参 数，除此之外，使用测量信号减去估计得到的可视距分量或强反射分量可得到漫散射分量， 本发明方法还可以准确的估计漫散射分量。 附图说明 图1是本发明所述方法一种可实施的流程图。 图2是本发明实施例的具体流程图。 图3是本发明实施例提供的方法估计出信道参数后重构的第z次快照的信道冲击 响应及估计到的漫散射分量。 图4是本发明实施例提供的方法与AR-SAGE算法信道参数估计结果的比较。 图5分别采用AR-SAGE算法与本发明提出的算法对余量信号进行滤波。 图6是本发明实施例提供的方法估计出到的漫散射分量通过ARIMA滤波后的功率 谱图。 图7是本发明实施例提供的方法与传统SAGE算法得到的剩余分量的累积周期图。