技术摘要：
本发明公开了一种交通速度预测方法、系统及存储介质，采集原始交通速度数据集，将所述数据集划分成训练集和测试集，挖掘原始交通速度数据集不同的空间关系，构建出两个路网图；将所述两个路网图的邻接矩阵融合为新图邻接矩阵；将所述训练集和所述新图邻接矩阵作为交通  全部
背景技术：
近年来，随着智能交通系统和全球定位系统(GPS)、移动设备等各种定位技术的快 速发展，交通数据的可获得性日益增强。从交通数据中挖掘有价值的知识对许多现实世界 的应用至关重要，包括智能交通、城市规划、公共安全等。交通预测对实现交通诱导，出行规 划和拥塞控制都具有重大的意义。所以如何进行实时准确的交通预测已经变得越来越受人 们关注。 交通预测问题被定义为基于道路网络中历史交通信息来预测未来某一个时间段 的交通信息。本发明重点关注交通速度信息，交通速度数据是一种时空数据，由于城市道路 网络拓扑结构的约束和动态变化的规律使得其具有复杂的时间和空间上的相关性。如何准 确全面的挖掘出交通速度数据之间的时空相关性是提高交通预测准确性的一个关键之处。 目前国内外有许多关于交通预测方法的研究，大致可以分为两类：传统的机器学 习方法和深度学习方法。 传统的机器学习方法的主要方法有，自回归积分移动平均模型ARIMA[1]，线性回 归模型[2]，以及为了改善预测精度提出的一系列ARIMA模型的变体，周期性ARIMA[3]，子集 ARIMA[4]。这些时间序列模型利用已观测到的时间序列去预测未来的数据。但是这些模型 依赖于假设系统模型是静态的，不能反映交通数据的非线性和不确定性，不能克服交通事 故等随机事件的干扰。因此有研究人员开始使用支持向量机回归模型[5]，贝叶斯网络模型 [6]和K近邻模型[7]等方法，这些方法可以自动的利用足够的历史数据来学习交通信息的 时间变化规律，克服了只支持静态系统的假设。 近年来，随着深度学习的快速发展，深度神经网络模型因能很好地捕捉交通数据 的动态特性而受到关注。比如卷积神经网络模型(CNN)[13]。在图像处理中，CNN表现出强大 的能力来建模像素之间的相似性，这也可以被看作为一种空间关系。在这个点的启发下，一 些研究者开始使用卷积神经网络(CNN)来捕捉交通网络之间的相邻关系，同时在时间轴上 使用递归神经网络(RNN)以及RNN的变体长短时记忆网络(LSTM)，门控递归单元(GRU)[14] 来提取时间特征。Zhang等人[8]提出了一种深度学习模型称为ST-ResNet,基于时间的邻近 性、周期性和趋势性来为这三个属性分别设计一个残差卷积网络,然后将三个网络和外部 因素动态整合来预测城市人流数。Wang等人[9]，将交通信息建模为一个时空矩阵，结合CNN 和RNN来预测道路交通速度和拥塞源，并且加入了一个误差反馈机制来对早晚高峰和交通 事故等突发事件进行建模，提高对道路交通速度预测的精度。由于道路更容易生成图的表 示，有研究人员开始关注图卷积神经网络模型(GCN)[15]。Zhao等人[10]提出的T-GCN模型 将每一个路段作为节点，根据路段是否相连形成边，生成一张路网图，利用图卷积网络GCN 和门控递归单元模型GRU分别捕获获得空间特征和时间特征来生成交通预测结果。Yu等人 [11]提出了一个STGCN模型，将每一个观测点作为节点，两个点之间的距离作为边生成路网 4 CN 111612243 A 说　明　书 2/10 页 图，利用两个时空卷积块来处理图结构化的序列交通数据，最终进行路网级的交通速度预 测。Geng等人[12]提出来一个ST-MGCN模型来进行网约车需求量的一个预测。文章使用图对 区域间的三种空间相关性进行了分别的建模。对三个图分别处理完时间序列之后再使用图 卷积神经网络进行空间特征的提取，最后进行特征的融合，最终生成需求量预测结果。 现有的方法在进行交通预测时存在着一些问题。使用传统的机器学习方法预测 时，考虑了交通信息随时间的动态变化但是却忽略了空间上的拓扑结构的改变，使得不能 准确的预测交通状态。而深度学习方法如CNN模型虽在建模空间相关性上有效,但是却由于 它只适用于欧几里得空间数据的局限性,使得其对路网拓扑关系的建模可解释性较差。图 卷积神经网络(GCN)模型的发展，为提取交通数据的空间关系提供了一种很好的解决方案。 而现有的图卷积神经网络模型在进行交通速度预测时，对交通速度数据的空间特征挖掘不 全面，大多考虑的只有相邻路段或者相邻区域的单一空间关系，而实际上空间上的关系存 在很多种，譬如还存在地图上相隔很远，但是交通需求模式或者拥堵模式非常相似的路段。 又或是像已有的ST-MGCN模型虽挖掘了诸多空间信息，但存在预测模型存在复杂度大，参数 多，收敛慢等问题。 [1]M.S.Ahmed  and  A.R .Cook“, Analysis  of  freeway  traffic  time-series  data  by  using  Box-Jenkins  techniques,”Transp.Res.Rec.,no.722,pp.1–9,1979. [2]Dudek ,Grzegorz .Pattern-based  local  linear  regression  models  for  short-term  load  forecasting[J] .Electric  power  systems  research ,2016 ,130 (JAN.):139-147. [3]Williams  B  M,Hoel  L  A.Modeling  and  Forecasting  Vehicular  Traffic  Flow  as  a  Seasonal  ARIMA  Process:Theoretical  Basis  and  Empirical  Results[J] .Journal  of  Transportation  Engineering,2003,129(6):p.664-672. [4]Lee  S,Fambro  D,Lee  S,et  al .Application  of  Subset  Autoregressive  Integrated  Moving  Average  Model  for  Short-Term  Freeway  Traffic  Volume  Forecasting[J].Transportation  Research  Record  Journal  of  the  Transportation  Research  Board,1999,1678(1):179-188. [5]Wu  C  H ,Wei  C  C ,Su  D  C ,et  al .Travel  time  prediction  with  support  vector  regression[C]//Intelligent  Transportation  Systems,IEEE.IEEE,2003. [6]Sun  S ,Zhang  C ,Yu  G .A  Bayesian  Network  Approach  to  Traffic  Flow  Forecasting[J].IEEE  Transactions  on  Intelligent  Transportation  Systems,2006,7 (1):p.124-132. [7]ZHANG  Xiao-li ,HE  Guo-guang ,LU  Hua-pu .Short-term  traffic  flow  forecasting  based  on  K-nearest  neighbors  non-parametric  regression[J].journal  of  systems  engineering,2009. [8]Zhang  J ,Zheng  Y ,Qi  D.Deep  Spatio-Temporal  Residual  Networks  for  Citywide  Crowd  Flows  Prediction[J].2016. [9]Wang  J ,Gu  Q ,Wu  J ,et  al .Traffic  Speed  Prediction  and  Congestion  Source  Exploration:A  Deep  Learning  Method[C]//IEEE  International  Conference  on  Data  Mining.IEEE,2016. 5 CN 111612243 A 说　明　书 3/10 页 [10]Zhao ,Ling ,Song ,Yujiao ,Zhang ,Chao ,等 .T-GCN:A  Temporal  Graph  ConvolutionalNetwork  for  Traffic  Prediction[J].2018. [11]Yu ,Bing ,Haoteng  Yin ,and  Zhanxing  Zhu ."Spatio-temporal  graph  convolutional  networks:A  deep  learning  framework  for  traffic  forecasting ." arXiv  preprint  arXiv:1709.04875(2017) . [12]Geng,Xu,et  al."Spatiotemporal  multi-graph  convolution  network  for  ride-hailing  demand  forecasting ."2019AAAI  Conference  on  Artificial  Intelligence(AAAI’19) .2019. [13]Krizhevsky  A,Sutskever  I,Hinton  G  E.Imagenet  classification  with  deep  convolutional  neural  networks[C] .Advances  in  neural  information  processing  systems.2012:1097-1105. [14]R.Fu,Z.Zhang ,and  L.Li“, Using  LSTM  and  GRU  neural  network  methods  f o r  t r a f f i c  f l o w  p r e d i c t i o n ,”i n  P r o c .3 1 s t  Y o u t h  A c a d e m i c  Annu.Conf.Chin.Assoc.Automat.(YAC) ,Wuhan,China,Nov.2016,pp.324–328. [15]Defferrard ,M.；Bresson,X.；and  Vandergheynst,P.2016.Convolutional  neural  networks  on  graphs  with  fast  localized  spectral  filtering.In  Advances  in  Neural  Information  Processing  Systems,3844–3852. [16]LI ,Yaguang ,et  al .Diffusion  convolutional  recurrent  neural  network:Data-driven  traffic  forecasting.arXiv  preprint  arXiv:1707.01926,2017.
技术实现要素：
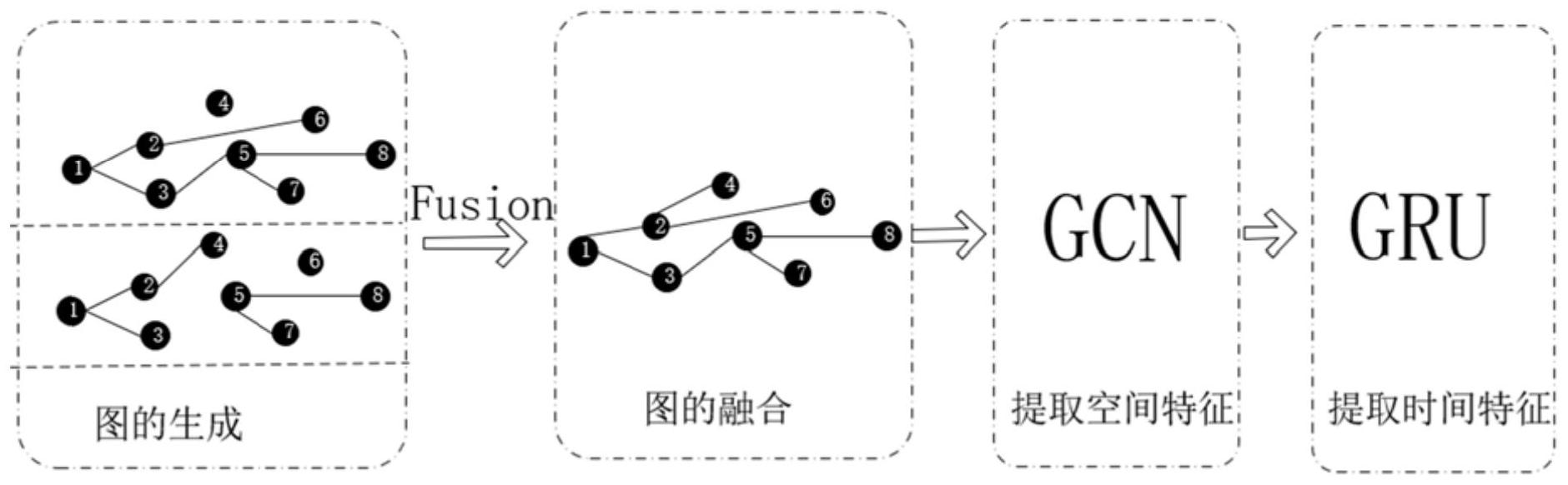
本发明所要解决的技术问题是，针对现有技术不足，提供一种交通速度预测方法、 系统及存储介质，充分全面的挖掘空间关系，减小模型处理的复杂度，准确预测交通速度。 为解决上述技术问题，本发明所采用的技术方案是：一种交通速度预测方法，其特 征在于，包括以下步骤： 1)集原始交通速度数据集，将所述数据集划分成训练集和测试集，挖掘原始交通 速度数据集不同的空间关系，构建出两个路网图； 2)将所述两个路网图的邻接矩阵融合为新图邻接矩阵； 3)将所述训练集和所述新图邻接矩阵作为交通预测模型的输入，训练得到预测模 型； 4)利用所述预测模型预测交通速度。 本发明将道路网建模为以图的形式，比使用卷积神经网络的方法相比更能抽象出 道路之间复杂的拓扑结构，为了能充分全面的挖掘空间关系，本发明构建出了两个不同的 路网图分别代表两种空间关系，将路网图的邻接矩阵融合，生成一个新图邻接矩阵，新图的 邻接矩阵就能够代表道路网中存在复杂的空间关系，减小处理多图的复杂度。 步骤1)中，所述两个路网图分别为邻居图和相关性图；所述邻居图GN＝(VN ,EN , AN)，其中，VN为邻接图的节点，EN代表邻接图的边，AN为邻居图的邻接矩阵；所述相关性图Gs ＝(Vs,Es,As)，其中，Vs为相关性图的节点，Es代表相关性图的边，As为相关性图的邻接矩 阵。本发明提取两种空间关系，邻居图代表了相邻相近互相影响的节点，而相关性图代表了 6 CN 111612243 A 说　明　书 4/10 页 不相邻但是依然能互相影响的节点，跟其它采用单图的方法相较而言，空间关系挖掘的更 全面，更能进行有效的预测。 所述邻居图的节点为道路或采集原始交通速度数据的传感器；当所述节点为道路 时， 当所述节点为传感器时， 其中vi ,vj代表传感器i和传感器j， dist(vi,vj)代表了传感器i和传感器j之间的距离，σ是传感器i和传感器j的距离之间的标 准偏差，k是为了保证邻接矩阵稀疏性设置的一个阈值。本发明采用了两种构建邻居图的邻 接矩阵的方法，分别应用于节点为道路或者传感器，增强了本发明方法的扩展性，可用于多 种类型的真实数据，两种构图方法均能有效的建模邻居空间关系。 所述相关性图的边的权值和邻接矩阵表达式如下： 其中ri,j代表相关性图节点(可以为道路或采集原始交通速度数据的传感器，若邻 居图节点为道路则相关性图的节点为道路，若邻居图节点为采集原始交通速度数据的传感 器，则相关性图的节点为采集原始交通速度数据的传感器)i和节点j之间的皮尔逊系数，Xi 代表节点i的速度向量， 代表节点i的速度向量的均值，Yi代表节点j的速度向量， 代表 节点j的速度向量的均值；As为相关性图的邻接矩阵；n是节点的个数。本发明采用皮尔逊相 关系数来计算节点之间速度向量的相关性，皮尔逊相关系数广泛用于度量两个变量之间的 相关程度，其值介于-1与1之间。相关系数的绝对值越大，说明两个向量线性相关的程度越 强。因为原始的交通速度数据集一般维度比较高，跟其它的计算相关性的方法如欧式距离 度量法和余弦相似度相比，更为简单且容错性更强。 步骤2)的具体实现过程包括： A)分别计算两个所述路网图的归一化的拉普拉斯矩阵； B)利用两个所述路网图的归一化的拉普拉斯矩阵分别计算两个所述路网图的谱 嵌入矩阵； C)根据每个路网图的谱嵌入矩阵和归一化的拉普拉斯矩阵，计算出新图的拉普拉 斯矩阵Lnew＝(LN LS)-(α1UNUN' α2USUS')；取出Lnew的对角线生成新图的度矩阵Dnew，根据公式 Anew＝Dnew-Lnew，求出新图的邻接矩阵Anew；其中，LN，Ls分别为两个路网图的归一化的拉普拉 斯矩阵；UN，Us分别为两个路网图的谱嵌入矩阵，UN'，US'分别为谱嵌入矩阵UN，Us的转置矩 阵，α1，α2为平衡等式项数的超参数。 7 CN 111612243 A 说　明　书 5/10 页 本发明采用路网图的归一化的拉普拉斯矩阵，对矩阵归一化是简化运算复杂度。 然后利用谱嵌入矩阵来进行降维操作，同样减少了运算复杂度，最后利用路网图的谱嵌入 矩阵和归一化的拉普拉斯矩阵，最终得出新图的拉普拉斯矩阵。与直接利用两个单图的方 法相比，这种融合方法处理得到的新图信息更丰富且有效，由于降维操作降低了计算的复 杂度，且删除了一些不重要的、冗余的影响预测结果的信息。 所述交通预测模型包括用于提取空间特征的图卷积神经网络和用于提取时间特 征的门递归单元。 深度学习方法如CNN模型虽在建模空间相关性上有效,但是却由于它只适用于欧 几里得空间数据的局限性,使得其对路网拓扑关系的建模可解释性较差。交通速度数据是 一种时空大数据，所以，交通预测模型需要同时提取空间特征和时间特征，由于本发明中道 路网用图的形式表示，图卷积神经网络(GCNN)自然成为该场景下的一种非常合适的提取空 间特征的选择，而提取时间特征的常用的方法，有递归神经网络(RNN)以及它的变体长短时 记忆网络(LSTM)和门控递归单元(GRU)，递归神经网络与长短时记忆网络相比，缺乏对长时 间的依赖关系的提取，长短时记忆网络和门控递归单元相比，参数多，收敛慢，因此在本发 明中选择用门控递归单元提取时间特征。所以本发明所述交通预测模型为提取空间特征的 图卷积神经网络和用于提取时间特征的门递归单元。 所述图卷积神经网络包括： 输入层，输入为所述原始交通速度数据集和所述新图邻接矩阵； 隐藏层，用于提取路网图中的空间特征，在新图邻接矩阵上做图卷积操作，图卷积 操作公式为： 其中X为原始交通速度数据集，Anew 为新图邻接矩阵， A～＝Anew I，I为单位矩阵；D～＝∑A～，D～即对应的A～ 的度矩阵；W0和W1分别是输入层到隐藏层的权值矩阵、隐藏层到输出层的权值矩阵。 输出层，用于输出图卷积操作的结果f(X,Anew)； 其中，隐含层和输出层的激活函数都为ReLU函数。 所述门控递归单元包括： 输入层，输入为t-1时刻从图卷积神经网络获得的输出结果f(Xt-1,Anew)以及t-1 时刻的隐藏状态ht-1，其中Xt-1代表t-1时刻原始交通速度数据集X的交通速度数据 隐藏层，用于根据t-1时刻从图卷积神经网络获得的输出结果f(Xt-1,Anew)以及t- 1时刻的隐藏状态ht-1，通过如下公式获取当前的隐藏状态ht： ut＝σ(Wu·[ht-1,f(Xt-1,Anew)]) rt＝σ(Wr·[ht-1,f(Xt-1,Anew)]) c＝tanh(Wc·[(rt*ht-1) ,f(Xt-1,Anew)])； ht＝(1-ut)*c ut*ht-1 其中，u是更新门，输入为t-1时刻从图卷积神经网络获得的输出结果f(Xt-1,Anew) 以及t-1时刻的隐藏状态ht-1，Wu是连接输入到更新门的权重矩阵，ut是更新门的输出；r是 复位门，输入为t-1时刻从图卷积神经网络获得的输出结果f(Xt-1,Anew)以及t-1时刻的隐 藏状态ht-1，Wr是连接输入层到复位门的权重矩阵，rt是复位门的输出；c是候选的隐藏状态 的值，输入为t-1时刻从图卷积神经网络获得的输出结果f(Xt-1,Anew)，以及复位门输出与 8 CN 111612243 A 说　明　书 6/10 页 t-1时刻的隐藏状态ht-1的乘积，Wc是连接输入和候选隐藏状态的权重矩阵；ht为当前的隐 藏状态；σ()是Sigmoid函数，tanh是双曲正切函数； 输出层，用于输出当前时刻的隐藏状态ht。 本发明图卷积神经网络和门控递归单元隐藏层节点数取值范围均为[16，128]，保 证误差大小合适，降低预测模型的复杂度。 本发明还提供了一种交通速度预测系统，包括计算机设备，该计算机设备被配置 或编程为用于执行上述方法的步骤。 作为一个发明构思，本发明还提供了一种计算机可读存储介质，其存储有程序，该 程序用于执行上述方法的步骤。 与现有技术相比，本发明所具有的有益效果为： 1、本发明能充分全面的挖掘空间关系，新图的邻接矩阵就能够代表道路网中存在 复杂的空间关系，减小处理多图的复杂度，能准确预测交通速度； 2、本发明预测模型相对现有技术较简单，训练过程计算量小，收敛快，实用性强。 附图说明 图1是本发明所提出的交通多图预测模型FMGCN的框架图； 图2是本发明采用的两层图卷积神经网络的示意图； 图3是本发明使用的门控递归单元的内部结构图； 图4是时空图卷积预测模型(TGCN)的内部结构图； 图5是基于多图的网约车需求预测模型(ST-MGCN)的网络结构图； 图6是5个模型的精度对比的条形图； 图7是本发明提出的预测模型使用单图的精度对比的条形图。