技术摘要：
本发明提供了一种考虑人车冲突的协同转向控制方法，基于一种驾驶员和协同转向控制器同时在环的驾驶模式，该模式下当驾驶员控制目标与协同转向控制器控制目标不一致产生控制冲突时，通过构建博弈关系使得驾驶员与协同转向控制器实现博弈平衡来削减控制冲突程度；驾驶过  全部
背景技术：
随着车辆智能等级提高，驾驶员辅助系统的能力不断提升，在特定情况下甚至无 需驾驶员干预完全控制车辆，但全域无人驾驶的实现是一个长期的过程，过早的应用无人 驾驶系统会给交通安全带来巨大威胁。以目前世界汽车行业水准来看，人们认为司机应该 将自己的手停留在方向盘上与驾驶辅助系统共同驾驶车辆，工业界和学术界正在努力设计 更具合作性的驾驶员在环人车共驾辅助系统，这些系统与传统的辅助系统相比，其创新性 在于人机共同控制车辆完成驾驶任务。 驾驶员行为有着个性化难以预测的特征，行车过程中人车之间难免出现意图不一 致，如何在人车目标不一致情况下，实现驾驶辅助系统和驾驶员之间实现最佳的低水平合 作仍然是个挑战。
技术实现要素：
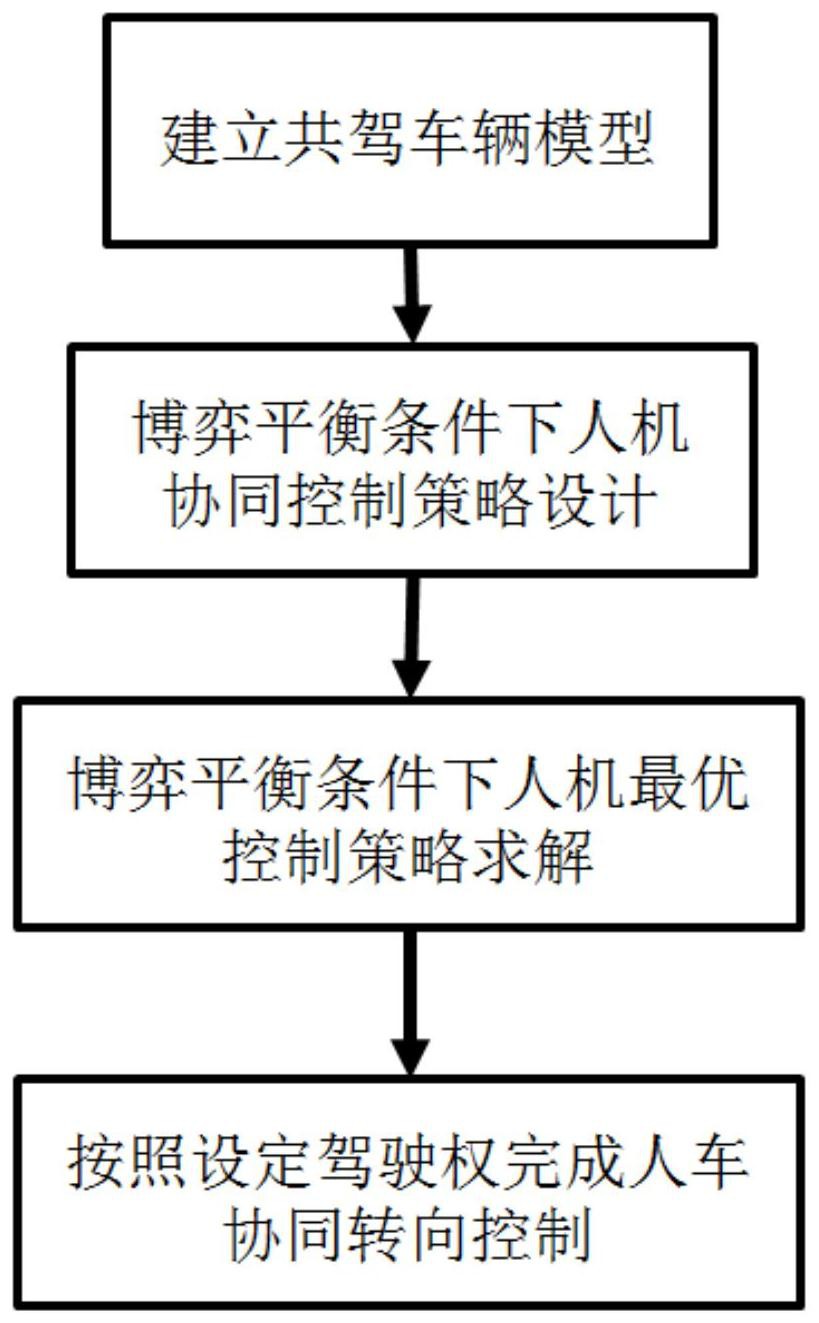
本发明为解决驾驶员与协同转向控制器在目标不一致条件下的控制冲突问题，提 出一种可以实现人车博弈平衡的协同转向控制方法。 本发明所述的一种考虑人车冲突的协同转向控制方法，是采用如下技术方案实现 的： 一种考虑人车冲突的协同转向控制方法，基于一种驾驶员和协同转向控制器同时 在环的驾驶模式，该种模式下当驾驶员控制目标与协同转向控制器控制目标不一致产生控 制冲突时，通过构建博弈关系使得驾驶员与协同转向控制器实现博弈平衡来削减控制冲突 程度，本方法具体步骤如下： 步骤一、建立共驾车辆系统模型： 建立大地坐标系：原点O固结于地面，X轴正方向为车辆初始运动方向，Y轴的正方 向为X轴逆时针旋转90度方向； 建立车辆坐标系：以车辆质心o为坐标原点，x轴的正方向为车辆前进的方向，y轴 的正方向为x轴逆时针旋转90度方向； 用车辆运动学模型表征车辆的操纵稳定性与车辆的侧向运动的关系，并用二自由 度车辆动力学模型表征车辆的操纵稳定性和车辆的横摆运动之间的关系，具体过程如下： 假定车辆是一个质量块，以车辆前轮作为转向轮，根据车辆运动学方程以及车辆 运动的几何关系得到车辆的运动学模型如式(1)所示： 9 CN 111717207 A 说　明　书 2/14 页 式中xo为车辆质心o的纵向位移，单位m；yo为车辆质心o的侧向位移，单位m；v为车 辆质心的速度，单位m/s；r为车辆的横摆角速度，单位rad/s；ψ为车辆的航向角，单位rad；β 为车辆的质心侧偏角，单位rad； 考虑到实际道路的曲率通常很小，车辆在实际行驶时航向角ψ同样可以认为是很 小的，且实际车辆的质心侧偏角β变化范围也很小，所以有：sin(ψ β)≈ψ β，cos(ψ β)≈1， 当车辆匀速行驶时可以忽略纵向车速的影响，同时结合式(1)可以得到简化的车辆运动学 模型，如式(2)所示： 本方法通过控制车辆的前轮转角来实现路径跟踪的目的，并且认为车辆保持匀速 状态行驶，所以只需要考虑车辆的侧向运动，根据牛顿第二定律与力矩平衡关系，可得到如 式(3)所示的二自由度车辆动力学模型： 式中vx为车辆质心处的纵向速度，单位m/s；Fyf为车辆前轮侧向力，单位N；Fyr为车 辆后轮侧向力，单位N；m为车辆的质量，单位kg；Iz为车辆绕z轴的转动惯量，单位kg·m2；a为 车辆质心o到车辆前轴的距离，单位m；b为车辆质心o到车辆后轴的距离，单位m；δf为车辆前 轮转角，单位rad； 车辆实际的前轮转角δf通常在小范围内变化，可以近似认为：cosδf≈1，sinδf≈0， 因此对式(3)进行简化，简化后的二自由度车辆动力学模型如式(4)所示： 车辆侧向轮胎力未达到饱和时，车辆侧向轮胎力Fy与轮胎侧偏角α可近似看作呈 线性关系如式(5)所示： 式中Cf为车辆前轮的轮胎侧偏刚度，单位N·rad；Cr为车辆后轮的轮胎侧偏刚度， 单位N·rad；αf为车辆前轮的轮胎侧偏角，单位rad；αr为车辆后轮的轮胎侧偏角，单位rad； 在车辆坐标系下，前轮的轮胎侧偏角αf和后轮的轮胎侧偏角αr有如式(6)的关系： 结合式(4)、式(5)和式(6)，整理可得式(7)： 10 CN 111717207 A 说　明　书 3/14 页 驾驶员和协同转向控制器之间的驾驶权重α可以根据驾驶员的意愿进行提前设 定,设定范围为0≤α≤1,驾驶员和协同转向控制器共同驾驶车辆时车辆前轮转角δf由两部 分组成，驾驶员当前时刻决策出的前轮转角δh，协同转向控制器当前时刻决策出的前轮转 角δa，后再按照式(8)给出的比例关系进行叠加执行到车辆的前轮： δf＝αδh (1-α)δa                        (8) 式中δa为当前时刻协同转向控制器前轮转角，单位rad；δh为驾驶员当前时刻前轮 转角，单位rad； 结合式(2)、式(7)和式(8)，由于侧向车速相对于纵向车速较小可以近似看作v≈ vx，整理可得共驾车辆系统模型如式(9)： 该共驾车辆系统模型选取车辆质心o的侧向位移yo作为人车协同转向系统的输 出，同时选取人车协同转向系统的辅助前轮转角δa作为人车协同转向系统系统模型的控制 输入，选取状态向量x＝[y To ψ β  r] ，人车协同转向系统模型可被描述成如式(10)所示的状 态空间形式： 其中A为系统矩阵，表示系统内部状态变量的关系；Ba为协同转向控制器的控制矩 阵，表示协同转向控制器的输入变量如何控制状态变量；表示输出变量如何反映状态；Bh为 驾驶员的控制矩阵，表示驾驶员的输入变量如何控制状态变量；C为输出矩阵，各个矩阵表 达式如下： 11 CN 111717207 A 说　明　书 4/14 页 C＝[1  0  0  0]； 为了方便控制器设计，将式(10)的共驾车辆系统模型进行离散化得到离散化以后 的共驾车辆系统模型如式(11)： 式中 T s为采 样时间，单位s； 步骤二、博弈平衡条件下人机协同控制策略设计： 驾驶员的决策过程与协同转向控制器类似，因此驾驶员和协同转向控制器均采用 预测控制进行决策，当依据驾驶员的驾驶能力和驾驶习惯选定驾驶权重后，驾驶员通过一 段时间的适应以后能够理解共驾车辆的特性和协同转向控制器辅助特性，在对协同转向控 制器动作预测的基础上实现自身的决策；协同转向控制器能够实时采集驾驶员的驾驶信 息，预测驾驶员未来的控制动作实现对驾驶员的辅助，驾驶员和协同转向控制器双方进行 决策都是基于式(11)的离散化以后的共驾车辆系统模型，定义Ca＝Ch＝Cc，依据预测控制原 理，定义预测时域为P，控制时域为N，驾驶员的预测输出方程如式(12)所示： Yh(k)＝Sh1x(k) Sh2Uh(k) Sh3Ua(k) .                 (12) 式(12)中的Yh(k)为预测时域内驾驶员预测的车辆侧向位移，Uh(k)为预测时域内 驾驶员决策的控制序列，Ua(k)为预测时域内驾驶员决策的控制序列协同转向控制器其状 态预测的基本原理与驾驶员类似，其预测方程如下所示： Ya(k)＝Sa1x(k) Sa2Uh(k) Sa3Ua(k) ,                  (13) 其中Ya(k)为预测时域内协同转向控制器预测的车辆侧向位移，式(12)与式(13) 中： 12 CN 111717207 A 说　明　书 5/14 页 驾驶员和协同转向控制器的决策可以表达为如下优化目标的形式： 驾驶员： 协同转向控制器： 式(14)中 为驾驶员的控制目标，式(15)中 为协同转向控制器的控 制目标，式(14)与式(15)中ya＝yh＝yo，Γhq、Γhr、Γaq与Γar分别为正定加权对角矩阵，Rh (k)为驾驶员的参考轨迹序列，Ra(k)为协同转向控制器的参考轨迹序列，通过传感感知模 块获取； 驾驶员和人机协同转向控制器的理想路径存在差别，即Rh(k)≠Ra(k)，则博弈双方 形成的为非合作博弈关系，当驾驶员和控制器双方都为了实现自身的期望路径而采取最优 控制策略时，此时人机之间的策略组合就构成了纳什均衡策略，当双方达成博弈平衡时满 足以下条件： 式中 为博弈平衡条件下驾驶员最优控制序列， 为博弈平衡条件下协同转向 控制器的最优控制序列，在转向控制的博弈过程中，如果驾驶员和协同转向控制器之间没 有进行最优路径之间信息沟通，驾驶员与协同转向控制器双方都没有改变自身最优控制量 的可能，因为单边改变自身最优控制量都会使得自身对参考路径的跟踪精度下降，因此达 到均衡条件时，驾驶员和协同转向控制器双方均达成了自身的最优控制策略，虽然这不一 定是全局条件下双方可能达到的全局最优策略，但一定程度上通过实现的博弈的平衡削减 了人机冲突的程度； 步骤三、博弈平衡条件下人机最优控制策略求解： 驾驶员的控制目标式(14)中 和协同转向控制器的控制目标式(15)中 进行转换则可以写成如下形式： 13 CN 111717207 A 说　明　书 6/14 页 上式(17)等价于 因此博弈平衡条件下驾驶员最优控制序列 和博弈平衡条件下协同转向控制 器最优控制序列 可以求得如下形式： 式(19)中博弈平衡条件下驾驶员最优控制序列 和博弈平衡条件下协同转向 控制器最优控制序列 相互耦合，博弈双方优化问题的求解需要已知对方优化的结果， 因此无法直接求解最优的控制策略，因此为了解决这个问题，可以添加如下凸迭代伴随方 程求解： 其中ω1与ω2为加权系数并且满足ω2 ω2＝1，p代表的是迭代的步数， 表 示迭代过程中第p步时的驾驶员的最优控制序列，U (k)[p]h 表示迭代过程中第p步时的驾驶 员的非最优控制序列，Uh(k)[p 1]表示迭代过程中第p 1步时的驾驶员的非最优控制序列， 表示迭代过程中第p步时的协同转向控制器的最优控制序列，Ua(k)[p]表示迭代过 程中第p步时的协同转向控制器的非最优控制序列，Ua(k)[p 1]表示迭代过程中第p 1步时的 协同转向控制器的非最优控制序列；当迭代步数一定时，其迭代的顺序如下：首先给定p＝0 时驾驶员和控制器的控制输入初值，式(19)可以用来求取p＝0时的“最优”人机控制输入， 利用式(20)可以求得p 1人机所采取的控制策略，以此循环往复；当迭代步数到达无穷时， 即p→∞, 时，将方程 和 代入式 14 CN 111717207 A 说　明　书 7/14 页 (19)可以求得： 其中： Δh＝(I-ΦhSh3ΦaS )-1h2 Φh,Δa＝(I-Φ -1aSh2ΦhSh3) Φa. 针对式(19)中若第一个矩阵奇异导致纳什均衡问题不可解的问题加以证明，考虑 加权矩阵Γhq、Γhr、Γaq、与Γar一般为正定对角阵，则矩阵 和 为列满秩 矩阵，则根据广义逆的性质： 可以看出 为对称满秩方阵，因此其逆也为对称满秩方阵，观 察矩阵 也为对称满秩矩阵，因此ΦhSh3则为对称满秩方阵，同理ΦaSh2 也为对称满秩方阵，则矩阵I-ΦhSh3ΦaSh2与矩阵I-ΦaSh2ΦhSh3也为对称满秩方阵，则式 (19)则必定有解； 步骤四、人车协同转向控制执行： 将步骤三中式(21)求解出的博弈平衡条件下驾驶员最优控制序列 中控制序 列的第一项和博弈平衡条件下协同转向控制器最优控制序列 中控制序列的第一项按 照式(8)求得当前时刻车辆前轮转角如式(23)： 当前时刻车辆前轮转角δf作为最终控制量传给车辆，车辆通过相应的执行机构执 行控制量δf，即可完成驾驶员控制目标和协同转向控制器控制目标发生冲突的条件下的协 同转向控制。 进一步的技术方案包括： 步骤二中驾驶员的参考轨迹序列Rh(k)通过求取均值的方法获得，具体是通过反 复采集驾驶员通过某一路段的行驶轨迹，将多次行驶轨迹进行叠加并求取均值获得。 15 CN 111717207 A 说　明　书 8/14 页 本发明的有益效果为： 1.本发明提出了一种考虑人车冲突的协同转向控制方法，在驾驶过程中驾驶员与 协同转向控制器目标不一致产生控制冲突时，使得人车之间实现博弈平衡来保证车辆安全 完成转向操作； 2.本发明利用博弈论重构驾驶员和协同转向控制器之间关系模型，驾驶员和协同 转向控制器目标不一致时通过预测对方的控制策略而采取自身最优的控制策略而实现博 弈平衡，博弈平衡改善了人机控制策略的冲突程度； 3.本发明根据重构驾驶员和协同转向控制器之间关系模型，使得驾驶员和协同转 向控制器能够依据设定的驾驶权重实现控制策略的自动调整。 附图说明： 图1为本发明所述的一种考虑人车冲突的协同转向控制方法的流程简图； 图2为本发明所述的一种考虑人机冲突的协同转向控制方法的原理示意图； 图3为车辆运动学模型的示意图； 图4为车辆二自由度动力学模型的示意图；