技术摘要：
本发明公开了一种旋转关节型工业机器人模态参数和振动响应计算方法，具体涉及旋转关节型工业机器人的振动特性分析与计算。主要包括：将工业机器人整体结构化整为零，拆分成具有传递关系的若干个元件；建立各个元件的传递矩阵和传递方程；根据元件传递链形成系统总传递  全部
背景技术：
工业机器人作为生产加工的重要工具和设备，其性能与动态特性紧密相关，从设 计生产到使用，对工业机器人进行动态特性分析至关重要。尤其是近年来，随着机器人加工 系统越来越多地被应用于航空航天高端制造领域，特别是在加工钛合金、镍基合金、复合材 料等难加工材料时，机器人加工系统极易产生颤振，影响制造加工质量，严重时甚至会导致 产品损坏，造成不可挽回的损失。因此，需要对机器人加工系统进行振动特性研究，计算其 模态参数和振动响应，分析机器人加工系统的动力学性能，为制定工艺路线和加工颤振抑 制策略提供理论指导。 在工业机器人结构设计过程中，常采用有限元仿真、模态分析等方法进行结构优 化，已公开发明专利“一种工业机器人大臂结构优化方法，CN110705170A”发明了一种工业 机器人大臂结构优化方法，对拓扑优化后的模型进行仿真模态分析，验证结构优化成果。该 方法依赖于仿真软件进行分析优化，需要不断对结构进行修改与调整，设计优化周期长，且 有限元分析依赖软件自带算法，无法根据实际需求对其进行改进计算。为了实现机器人的 振动抑制，发明专利“一种空间柔性机械臂振动抑制算法，CN201610549912.3”在广义坐标 系下建立机械臂系统的动力学模型，分解了动力学变量并设计了挠性振动控制器以实现振 动抑制，该方法需要建立机械臂整体动力学模型，建模方法复杂，计算速度慢。综上所述，现 有工业机器人振动特性分析存在结构优化依赖仿真分析、动力学方程复杂、振动响应计算 速度慢等不足。本发明针对上述缺点，提出了一种旋转关节型工业机器人模态参数和振动 响应计算方法。
技术实现要素：
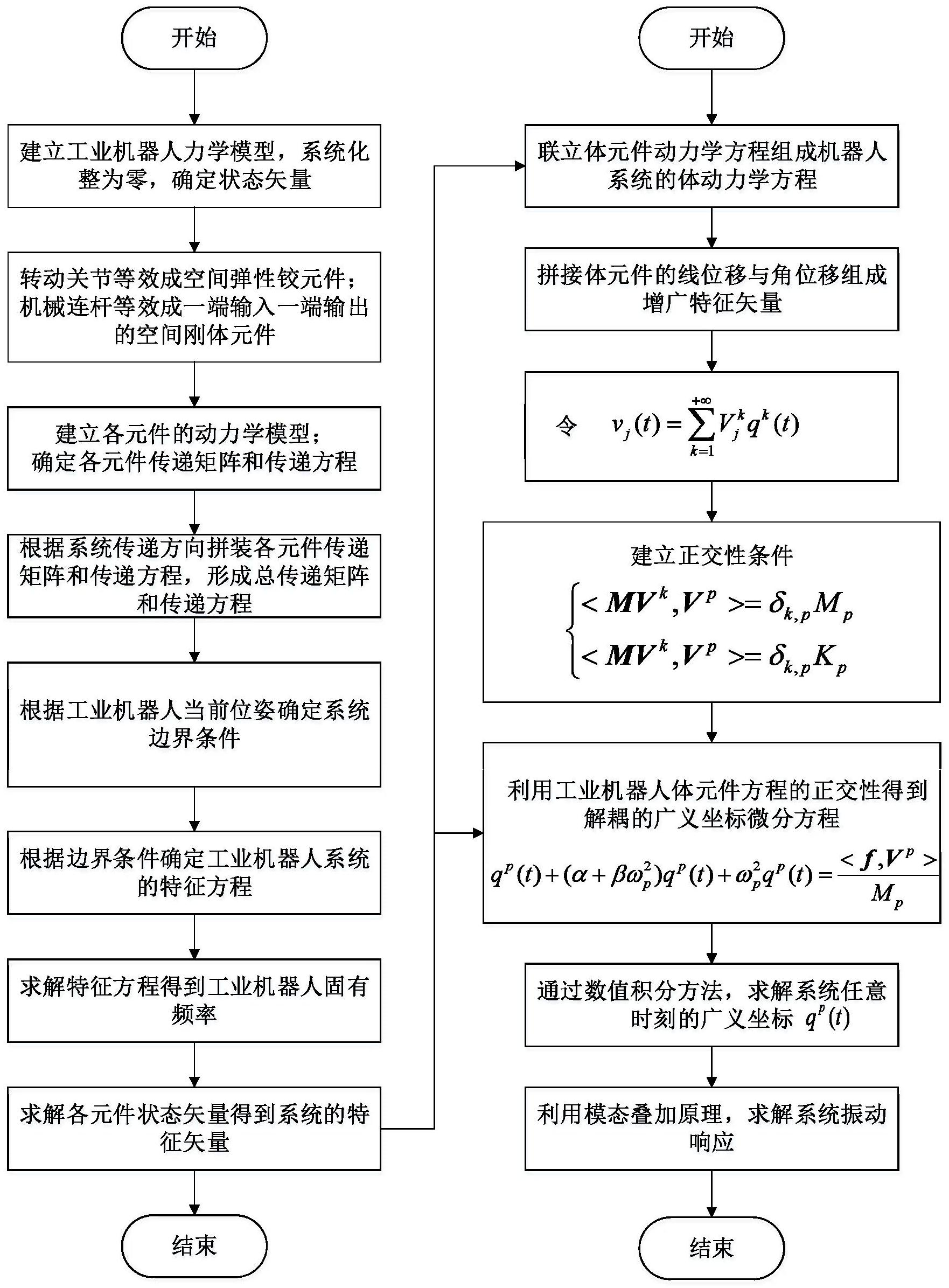
本发明所要解决的技术问题是针对上述现有技术的不足，提供一种旋转关节型工 业机器人模态参数和振动响应计算方法。 为实现上述技术目的，本发明采取的技术方案为： 一种旋转关节型工业机器人模态参数和振动响应计算方法，包括如下步骤： 步骤一：提取待建模的工业机器人系统的主要结构元件，包括机械连杆和转动关 节，并对各元件进行统一编号； 步骤二：建立物理坐标和模态坐标，定义物理坐标和模态坐标下的各个转动关节 和机械连杆的状态矢量； 步骤三：建立机械臂杆件和转动关节的动力学模型，根据机械臂杆件和转动关节 的基本参数，分别计算各机械臂杆件和转动关节的传递矩阵和传递方程； 步骤四：结合各机械臂杆件和转动关节的传递矩阵和传递方程，计算工业机器人 4 CN 111597657 A 说　明　书 2/8 页 的总传递矩阵和总传递方程； 步骤五：根据工业机器人实际边界特性，计算工业机器人边界条件； 步骤六：确定系统特征方程，求解特征方程得到工业机器人各阶固有频率与振型； 步骤七：根据工业机器人增广特征矢量，利用模态叠加原理和增广特征矢量正交 性，计算得到机器人振动响应。 为优化上述技术方案，采取的具体措施还包括： 进一步地，步骤一中，将机械连杆等效为空间刚体元件，将转动关节等效为空间弹 性铰元件，定义边界点为零，对转动关节与机械连杆按照实际安装顺序依次编号。 进一步地，步骤二中，各个转动关节和机械连杆在物理坐标、模态坐标下的状态矢 量分别为： 式中，x、y、z表示物理坐标下惯性坐标系中联接点相对于其平衡位置的线位移； θx、θy、θz表示物理坐标下惯性坐标系中联接点相对于其平衡位置的角位移；mx、my、mz表示物 理坐标下联接点处的内力矩；qx、qy、qz表示物理坐标下联接点处的内力；X、Y、Z，Θx、Θy、 Θz，Mx、My、Mz，Qx、Qy、Qz分别为对应小写字母物理量的模态坐标，i，j表示相邻元件序号 进一步地，步骤三具体为： 建立各转动关节的传递矩阵和传递方程，确定其输入端为Ij，输出端为Oj，其传递 方程表示为： Zj，O＝UjZj，I 式中，Uj为转动关节j的传递矩阵， 和 分别为转动关节j的输出端和输入端的 状态矢量； 建立各连杆的传递矩阵和传递方程： 确定其输入端为Ii，输出端为Oi，其传递方程可以表示为： Zi，O＝UiZi，I 式中，Ui为连杆i的传递矩阵， 和 分别为连杆i的输出端和输入端的状态矢 量。 进一步地，步骤四具体为： 计算工业机器人的总传递矩阵： Uall＝UnUn-1KU2U1 计算工业机器人的总传递方程： Zn，0＝UallZ1，0 式中，Uall为系统总传递矩阵。 进一步地，步骤六具体为： 根据工业机器人实际边界特性，确定工业机器人边界条件 式中，Zn，0为第刀个元件的输出端的状态矢量，Z1，0表示第一个元件的输入端的状 5 CN 111597657 A 说　明　书 3/8 页 态矢量。 进一步地，步骤七具体为，将边界条件代入总传递矩阵： 求解工业机器人的各阶固有频率： 根据Zn，0和Z1，0中的零元素简化得到系统特征矩阵 k为固有频率的阶次 求解满足 对应的行列式的值为0的ωk的值，计算得到工业机器人的各阶固有频 率ωk； 求解工业机器人的各阶振型： 将各阶固有频率值代入机械连杆和转动关节的传递矩阵和传递方程，计算得到各 元件在模态坐标下的状态矢量，即可得到机械连杆和转动关节的振型。 本发明的有益效果： 本发明一种旋转关节型工业机器人模态参数和振动响应计算方法，通用性好，建 模灵活且程式化程度高，通过对组成工业机器人的每个元件独立建模，分别计算各元件的 传递矩阵和传递方程后，按照实际连接顺序传递得到系统的总传递矩阵和总传递方程，同 时拼接后形成的总传递矩阵的阶次不随着系统自由度的增加而增大，这就有效提高了计算 速度，实现模态参数和振动响应的快速计算。 附图说明 图1工业机器人振动特性分析与振动响应计算的流程图； 图2为工业机器人动力学模型及其拓扑图； 图3为空间弹性铰模型示意图； 图4为一端输入一端输出的空间振动刚体模型示意图。