技术摘要：
一种基于低秩张量链分解的图像修复方法，包括获取破损的观测图像，确定破损图像中待修复区域的所有未知像素点的集合Ω；构建一种基于低秩张量核范数链分解的图像修复模型TNN‑TT，引入全变分，构造加权张量Schatten P范数并作为张量秩的非凸松弛，构建一种基于低秩张量  全部
背景技术：
随着人类社会的进步以及科技的发展，人们每天通过数字媒介获取数以亿计的信 息，包括图像、语音以及文本等。据统计，人类获取的信息约75％是通过视觉感知系统获得 的。图像作为视觉传输的主要载体之一，在人们进行交流通信以及视觉感知过程中起着至 关重要的作用。 图像在获取、存储与传输过程中不可避免地丢失一些信息，例如在获取遥感图像 时，由于传感器损坏或者天气影响等因素使得获取的遥感图像出现条带噪声或者有用信息 被云层遮挡等。图像修复是指对受到损坏的图像进行修复重建或去除图像中的多余物体， 图像修复已成为在图像后续应用前必不可少的预处理步骤。 围绕图像的修复问题，国内外研究者们提出了很多的修复方法。第一类是基于低 秩性的方法。高维图像可以看作一个天然的张量，利用所有维度的低秩性能有效恢复图像。 第二类是基于局部平滑性的方法。除了低秩先验，而实际图像数据常常表现出分段光滑的 性质。全变分(Total  Variation，TV)能够很好地刻画分段光滑的性质，并且被证明其在图 像复原中表现优异。第三类是基于相关性的方法。张量虽然能够比矩阵更详细地记录高维 图像各维度的信息，但如何定义精确刻画各维度相关性的仍是一个开放问题，经典的张量 分解方法有CP分解，Tucker分解和张量链分解(Tensor  Train  decomposition，TT)。
技术实现要素：
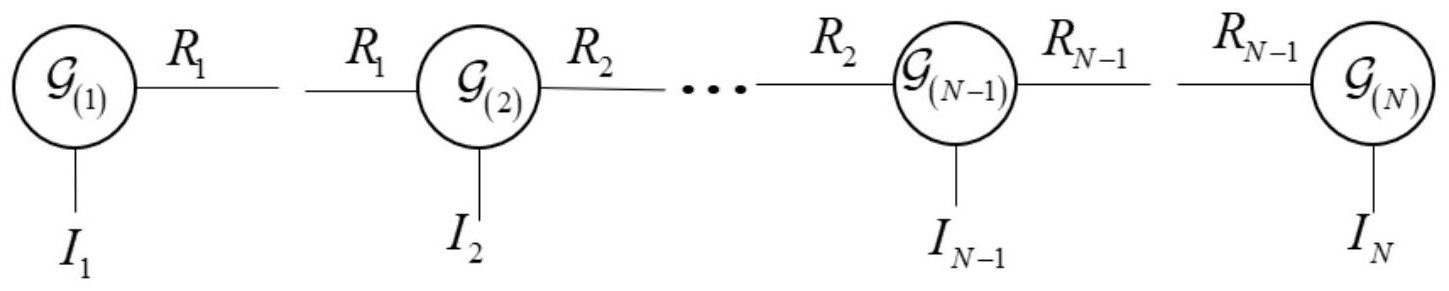
为进一步提高图像修复的效果，本发明提供了一种基于低秩张量链分解的图像修 复方法。 本发明解决其技术问题所采取的技术方案如下： 一种基于低秩张量链分解的图像修复方法，所述方法包括以下步骤： 步骤1)获取破损的观测图像，确定破损图像中待修复区域的所有未知像素点的集 合Ω； 步骤2)考虑图像张量所有维度的低秩性和相关性，结合张量核范数和张量链分 解，构建一种基于低秩张量核范数链分解的图像修复模型，记为TNN-TT模型； 步骤3)引入能够很好地刻画分段光滑性，并且被证明其在图像复原中表现优异的 全变分，以TNN-TT模型为框架，构造加权张量Schatten  P范数并作为张量秩的非凸松弛，构 建一种基于低秩张量链分解的加权张量Schatten  P范数与全变分图像修复模型，记为 WTSTV-TT模型； 步骤4)为消除矩阵数据之间的相关性，引入辅助变量 优化所述 图像修复模型WTSTV-TT； 5 CN 111598798 A 说　明　书 2/7 页 步骤5)采用ADMM算法求解所述图像修复优化模型，获得修复后的图像 进一步，所述步骤2)的处理过程如下： 首先，考虑图像所有维度的低秩性，所采用的张量核范数定义如下： 其中， 表示待恢复的图像，其中I1,I2,...,IN是张量每一阶的维度， 表示实数，αi是非负权重且满足 是张量 第i维度的展开矩阵； 又考虑图像的相关性，采用的张量链分解的定义如下： 其中， 是表示张量链中的一个张量核，×1表示张量链 核的约减乘运算，Rn表示第n个秩，特别的定义R0＝RN＝1； 进而构建一种基于低秩张量核范数链分解的图像修复TNN-TT模型： 其中，γ是低秩范数的系数， 表示破损的图像； 进一步，所述步骤3)的处理过程如下： 引入能够很好地刻画分段光滑性，并且被证明其在图像复原中表现优异的全变 分，全变分的定义如下： TV(x)＝∑i＝1∑j＝1|x(i,j)|    (4) 其中，|·|表示L2范数，x(i,j)表示图像中的像素值； 下面定义第i层矩阵的加权Schatten  P范数： 其中，r(i)是矩阵 的秩， 是矩阵 的第j个奇异值， 是空 间权重矩阵，wi是权重w第i个元素； 进而得到张量 的加权Schatten  P范数： 其中，p(0≤p≤1)为Schatten-p范数的参数； 进而构建一种基于低秩张量链分解的加权张量Schatten  P范数与全变分图像修 复WTSTV-TT模型： 6 CN 111598798 A 说　明　书 3/7 页 其中，τ是一个非负的正则参数，λi是非负权重且满足 D(i)表示(Ii-1)-by- Ii的矩阵，[D(i)]j,j＝1，[D(i)]j,j 1＝-1，且D(i)中的其他元素为等于0； 进一步，所述步骤4)的处理过程如下： 引入辅助变量 所述图像修复模型WTSTV-TT优化为： 进一步，所述步骤5)的处理过程如下： (5-1)建立 在ADMM算法下的子问题： 其中，μ1是惩罚系数，Λ是拉格朗日乘子， 是Frobenius范数；(5-2)建立 在ADMM算法下的子问题： 其中，μ2是惩罚系数，Φ是拉格朗日乘子； (5-3)建立 在ADMM算法下的子问题： 其中，μ3是惩罚系数，Γ是拉格朗日乘子； (5-4)建立χ在ADMM算法下的子问题： 其中，μ4是惩罚系数，Ψ是拉格朗日乘子； (5-5)更新拉格朗日乘子： 7 CN 111598798 A 说　明　书 4/7 页 (5-6)更新惩罚系数： μ1＝κμ1,μ2＝κμ2,μ3＝κμ3,μ4＝κμ4    (14) 其中，k∈[1,1.5]是个常数。 本发明的有益效果是：(1)考虑了图像的低秩张量特性和相关性(2)考虑了图像的 局部平滑性(3)有良好的图像修复效果。 附图说明 图1是本发明的图像张量链分解的示意图； 图2是本发明方法的流程图。