技术摘要：
本发明公开了一种基于GBP的PSO方法，上述方法能解决现有技术存在的数据标签的实际标签生成和标签生成的准确性上不断存在准确性和待优化的问题，而标签对应内容的准确性对匹配和推荐的结果值影响很大，本发明在此引入粒子群算法来解决GBP数据标签的准确性和标签不断优化  全部
背景技术：
随着电子商务网站的快速发展，推荐系统已经被广泛研究和应用，推荐系统通过 提取分析用户的资料、行为、评分等信息，获得用户的喜好，来帮助电商找到特定的用户为 其推荐可能购买的产品，增加商品的销售量。 推荐系统通过收集用户的历史评分、交互(浏览、收藏、“点赞”，“踩”等交互行为)、 用户肖像(年龄、职业、性别等)、社交网络和上下文(时间、位置、活动状态、周围人员等)等 数据，对用户的历史兴趣及偏好进行分析，挖掘出用户喜欢的项目(视频、音频、书籍、菜品、 Web服务等信息)，然后主动地将相关信息推荐给用户，满足用户的个性化需求。推荐算法是 推荐系统的核心，很大程度上决定了推荐系统的性能。目前主要的推荐算法包括基于内容 的推荐、基于知识的推荐、基于关联规则的推荐、协同过滤推荐和组合推荐等。 目前被广泛研究的推荐系统有的是采用基于内容的推荐算法、协同过滤推荐算法 等。基于内容的推荐算法是通过用户购买过的产品的特征，为用户推荐与其相似的产品。这 种算法的优点是可以处理冷启动问题，处理新加入的产品，并且这种算法不会受到打分稀 疏性的问题，因为它不依赖于用户对产品的评分。但是它的缺点是无法处理像图形、视频和 音乐这种难以分析提取内容特征的商品。 协同过滤算法则是利用用户-产品评分矩阵，计算用户或产品之间的相似度，利用 相似度较高的邻居对其他产品进行评分预测，并根据预测评分的高低为目标用户进行推 荐。但是每一个用户购买的产品数量通常不到产品总数的1％，所以造成用户-产品评分矩 阵非常稀疏，从而使得推荐结果不佳；而基于邻域的协同过滤推荐算法是应用最早的协同 过滤推荐技术，代表性算法为基于用户的协同过滤推荐和基于项目的协同过滤推荐。然而 随着用户规模和项目数量的快速增长，基于邻域的协同过滤推荐算法的计算量大规模增 大，同时产生了严重的评分数据稀疏性问题，即评分稀疏性问题。为了处理可扩展性和评分 稀疏性问题，一些研究学者提出采用基于矩阵分解模型的推荐算法。矩阵分解模型假定“用 户—项目”评分矩阵可以被分解为低维的潜在特征矩阵的乘积，其中潜在特征用于表示用 户偏好或项目特征，如在电影推荐中，这些特征可能为喜剧、悬疑剧、爱情剧因素等。多次国 际性比赛和大量研究都验证了矩阵分解模型具有抗数据稀疏性、易编程、较低的时空复杂 度、较高的推荐精度和良好的可扩展性等优点。 虽然上述推荐方法各有优势，但是，上述推荐方法因为随着机器学习模型越来越 复杂，参数越来越多，很难求出一个具体的公式直接解出最佳的优化参数。 G-PSO算法属于进化算法的一种，和模拟退火算法相似，它也是从随机解出发，通 3 CN 111581525 A 说　明　书 2/5 页 过迭代寻找最优解，它也是通过适应度来评价解的品质，但它比遗传算法规则更为简单，它 没有遗传算法的“交叉”(Crossover)和“变异”(Mutation)操作，它通过追随当前搜索到的 最优值来寻找全局最优，并且在解决实际问题中展示了其优越性。 算法初始化为一群随机粒子(随机解)，然后通过迭代找到最优解，在每一次叠代 中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫 做个体极值pBest，另一个极值是整个种群找到的最优解，这个极值是全局极值gBest；另外 也可以不用整个种群而只是用其中一部分最优粒子的邻居，那么在所有邻居中的极值就是 局部极值，从而完成推荐最优解；现有技术的不足：某些问题上性能不是最好，有一定的待 优化空间；网络权重的编码而且遗传算子的选择有时比较麻烦； GBP数据标签的实际标签生成和标签生成的准确性上不断存在准确性和待优化的 问题，因为标签对应内容的准确性对匹配和推荐的结果值影响很大，所以在此引入粒子群 算法来解决GBP数据标签的准确性和标签不断优化的问题； 设想这样一个场景：一群鸟在随机搜索食物。在这个区域里只有一块食物。所有的 鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优 策略是什么呢。最简单有效的就是搜寻目前离食物最近的鸟的周围区域； 鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位 置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个 鸟群，最终，整个鸟群都能聚集在食物源周围，即找到了最优解； PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的 粒子都有一个由被优化的函数决定的适应值(fitnessvalue)，每个粒子还有一个速度决定 他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索； PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代 中，粒子通过跟踪两个"极值"来更新自己。第一个就是粒子本身所找到的最优解，这个解叫 做个体极值pBest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gBest。 另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值 就是局部极值； 再通俗点的场景描述；粒子群算法的基本思想是通过群体中个体之间的协作和信 息共享来寻找最优解。如上的情景。试着想一下一群鸟在寻找食物，在这个区域中只有一只 虫子，所有的鸟都不知道食物在哪。但是它们知道自己的当前位置距离食物有多远，同时它 们知道离食物最近的鸟的位置。想一下这时候会发生什么？同时各只鸟在位置不停变化时 候离食物的距离也不断变化，所以每个鸟一定有过离食物最近的位置，这也是它们的一个 参考。所以，粒子群算法就是把鸟看成一个个粒子，并且他们拥有位置和速度这两个属性， 然后根据自身已经找到的离食物最近的解和参考整个共享于整个集群中找到的最近的解 去改变自己的飞行方向，最后我们会发现，整个集群大致向同一个地方聚集。而这个地方是 离食物最近的区域，条件好的话就会找到食物； 那么这种实际应用场景和基因GBP数据标签之间根据粒子群算法的基础特性将安 我基因本身的数据进行清洗，作为算法开始前的数据样本，通过迭代寻找最优解，其实它追 随当前搜索到的最优值来寻找全局的最优。 数据标签的优化问题是产品设计和研发中最经常遇到的问题，许多问题最后都可 4 CN 111581525 A 说　明　书 3/5 页 以归结为优化问题，为了解决GBP数据标签的准确性和优化问题，所以在此引入粒子群算法 利用其目前已经被广泛应用的函数优化和神经网络训练的这些应用领域来不断优化基因 G-PSO算法。
技术实现要素：
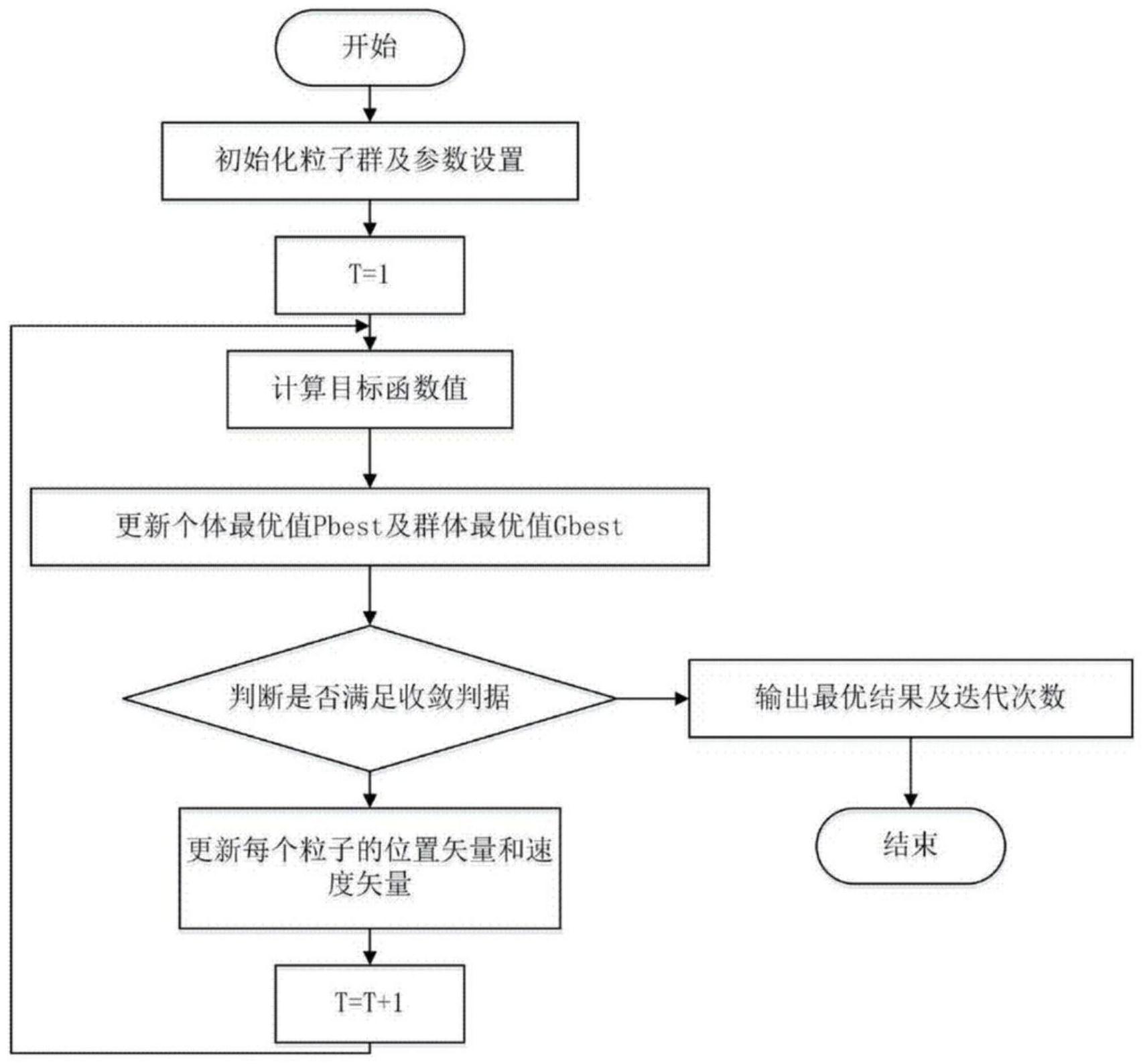
本发明所要解决的技术问题在于针对上述现有技术中的不足，提供一种基于基因 检测的粒子群算法的推荐方法，该算法在粒子群算法的基础上，通过将用户的基因(Gene)， 行为(Behavior)，表型(Phenotypic)这三类信息称之为用户的GBP数据，将这些数据进行标 签化，进而形成以用户为基础的GBP标签；本发明中将上述算法称为G-PSO算法，G-PSO算法 具有以下几个特点：演化计算优势，能处理一些传统方法不能处理的问题例如SCD；对与种 群适应值可以直接复制；对于单个个体计算适应值，并可以得到最优解。 为实现上述发明目的，本发明采用如下的技术方案： 一种基于基因检测的粒子群算法的推荐方法，包括以下步骤： 1)根据用户的GBP数据对用户进行标签化，每个用户就都拥有了各自的GBP标签， 每个标签代表一个不同的item； 2)对内容进行手动打标签，使内容也拥有了一个或多个标签： 3)根据用户的标签和内容标签进行初步的匹配，经过用户使用、反馈和算法校准， 用户已经对一些item做出了喜好判断，喜欢其中的一部分item，不喜欢其中的另一部分； 4)通过用户过去的喜好判断，为用户形成一个通用模型，后续根据用户的实习操 作的数据反馈进行标签权重系数的调整进而优化推荐系统的推荐机制： 5)商品推荐，通过上述通用模型，就可以判断用户是否会喜欢一个新的item，最终 得到推荐结果； 其中，所述的内容为文章、视频、商品、图片等； 其中，通用模型的目标函数较难优化时，采用基于基因检测的粒子群算法进行优 化； 其中，所述的基于基因检测的粒子群算法是用于求出目标函数的最优解，其求解 过程包括如下步骤： (1)初始化：首先，设置最大迭代次数，目标函数的自变量个数，粒子的最大速度， 位置信息为整个搜索空间，我们在速度区间和搜索G空间上随机初始化速度和位置，设置粒 子群规模为M，每个粒子随机初始化一个飞翔速度； (2)个体极值与全局最优解：定义适应度函数，个体极值为每个粒子找到的最优 解，从这些最优解找到一个全局值，叫做本次全局最优解，与历史全局最优比较，进行更新； (3)更新速度和位置； (4)根据GBP粒子相对最优值，做最优解最终得到结论； 其中，在找到这两个最优值时,粒子根据如下的公式来更新自己的速度和新的位 置，具体为：v[ ]＝v[ ] c1*rand( )*(pbest[ ]-present[ ]) c2*rand( )*(gbest[ ]- present[ ])(a)； present[ ]＝present[ ] v[ ](b)； 其中，v[ ]是粒子的速度,present[ ]是当前粒子的位置； 5 CN 111581525 A 说　明　书 4/5 页 其中，第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest[ ]，另一 个极值是整个种群找到的最优解，这个极值是全局极值gBest[ ]；另外也可以不用整个种 群而只是用其中一部分最优粒子的邻居，那么在所有邻居中的极值就是局部极值，从而完 成推荐最优解；rand( )是介于(0，1)之间的随机数； c1,c2是学习因子； 通常c1＝c2＝2； 本发明与现有技术相比具有以下优点：上述推荐方法具有演化计算优势，能处理 一些传统方法不能处理的问题例如SCD；对与种群适应值可以直接复制；对于单个个体计算 适应值，并可以得到最优解。 附图说明 图1为本发明中的流程图；